Nel campo del Computer Graphics, il CAD (o progettazione assistita da calcolatore) ha ormai raggiunto uno stadio di relativa maturità. Necessariamente relativa visto il forte sviluppo tuttora in corso sia dell'hardware che del software, ma del resto con linee di sviluppo chiare, due decenni di esperienza alle spalle, un mercato valutabile in migliaia di miliardi, un nutrito numero di specialisti, sufficiente a garantire trasmissibilità alle informazioni e solidità alla ricerca.
Nato agli inizi degli anni sessanta come tecnigrafo elettronico bidimensionale, il CAD si è evoluto alle tre e addirittura alle quattro dimensioni (il tempo!), fornendo l'animazione in tempo reale di scene anche complesse. Da qualche anno è poi in commercio una workstation grafica che consente di osservare i componenti grafici in stereoscopia risolvendo parzialmente il problema di rappresentare oggetti tridimensionali sul piano dello schermo video.
Parallelamente nel campo hardware i costi si sono ridotti con un ritmo di un dimezzamento ogni due o tre anni: infatti oggi per progettare una automobile è, al limite, possibile utilizzare una attrezzatura che costa poco più dell'automobile stessa.



LA MODELLAZIONE TRIDIMENSIONALE

Nel campo metodologico si sono affermati quattro sistemi di modellazione tridimensionale:
- Boundary surfaces o modellazione per superfici e contorni.
- Constructive Solid Geometry (CSG) o modellazione solida.
- Sweeping, "spazzolamento" traslazionale, rotazionale o generalizzato.
- Octree o modellazione per cubi elementari.

- BOUNDARY SURFACES. Il trattamento di solidi avviene non come insieme di punti (wire-frame) ma di superfici e contorni (boundary). Elimina i problemi del wire-frame ma risulta particolarmente difficoltoso per l'utente definire solidi complessi, perciò, di norma, questa rappresentazione viene ottenuta automaticamente, da programma, da altre a più alto livello, soprattutto per visualizzare gli oggetti vettorialmente (su plotter).

- CONSTRUCTIVE SOLID GEOMETRY. Uno degli ultimi sviluppi della modellazione tridimensionale è rappresentato dalla geometria solida. Questa parte dall'assunto che oggetti, anche molto complessi, possono essere visti come unione, intersezione, complemento e differenza di solidi elementari (primitive) come il cubo, la sfera, il cilindro o il cono. Di un oggetto non vengono memorizzate le coordinate ma la sequenza di operazioni (dette booleane) che portano alla sua definizione.

- SWEEPING. Molti solidi possono essere definiti da superfici in movimento, sia traslazionale che rotazionale. Ad esempio un cilindro è rappresentabile da un cerchio che si sposta lungo un asse perpendicolare al diametro o un cono da un triangolo rettangolo che ruota di 360 gradi attorno ad un cateto.
Lo sweeping (letteralmente spazzolamento) permette di definire solidi mediante varie associazioni di figure piane e spostamenti: i programmi più raffinati consentono non solo di variare liberamente la traiettoria ma anche, contemporaneamente, la forma della figura di sweeping: un solido sarà così memorizzato come una sagoma bidimensionale di partenza e una serie di equazioni che in ogni istante restituiscono la posizione tridimensionale del baricentro della figura (o di un altro punto) e le variazioni (bidimensionali) dei punti che costituiscono la figura stessa.
Una colonna scanalata potrà in questo modo essere vista come una sezione orizzontale di base, una traiettoria rettilinea verticale e una variazione di scala continua, funzione dell'altezza.

- OCTREE. Viene utilizzato per la definizione di volumi irregolari e privi di forti simmetrie quali, in architettura, statue, capitelli, fregi.
Se supponiamo di immergere il solido da modellare in un cubo che lo contenga completamente e di suddividere il volume in un numero considerevole di celle, anch'esse cubiche, più piccole (dette voxel); ogni cella potrà essere interna, esterna o intersecare il bordo del solido.
La sola conoscenza dello stato di tutti i voxel definirà il solido tanto più fedelmente quanto più piccolo sarà il voxel stesso, così come una fotografia risulta tanto più dettagliata e nitida quanto più fine è la grana.
Un difetto di quest'ultimo schema modellativo è la grande quantità di memoria necessaria e il fatto che una volta scelta la risoluzione questa non possa essere più cambiata pena il ripartire da zero nella modellazione.

Lo sweeping e la CSG possiedono, rispetto agli altri metodi, caratteristiche particolarmente interessanti: semplicità di interfaccia con l'utente, rapidità di costruzione e cambiamento, versatilità, icasticità rappresentativa, scarsa occupazione di memoria.



IL RILIEVO

Nello specifico campo del rilievo di architetture, soprattutto se storiche, si riscontrano, però, oggettive difficoltà nell'introdurre queste metodiche: alcuni impedimenti sono probabilmente da ricercare nel fatto che, provenendo le nuove idee (ed i relativi packages applicativi) in gran parte dall'estero (e dagli USA in particolare), è però in Europa, e in Italia soprattutto, dove si sente la necessità di rilevare, documentare e archiviare il grande patrimonio storico-artistico disponibile.
Inoltre sussiste una fondamentale dicotomia tra la progettazione e il rilievo assistiti da computer: mentre la prima procede nel campo della geometria euclidea, astratta, dove il disegno è una rappresentazione dell'idea di un oggetto architettonico; il rilievo possiede un referente esistente del quale deve, o dovrebbe, dare il maggior numero e qualità di indicazioni.
La progettazione rappresenta un iter a più entrate ma ad unica uscita (il progetto), il rilievo, al contrario, deve permettere il percorso inverso e rispondere alle domande più disparate poste dallo storico, dall'architetto, dallo strutturista, dal restauratore.
Esistono, infine, anche difficoltà più prosaiche e pratiche che si oppongono ad un uso completo del computer nel rilievo: in un edificio, soprattutto se di epoca non recente, ogni metopa, ogni lesena, ogni finestra pur se identica tipologicamente e nel progetto alle sue vicine, è nella realtà metricamente diversa, traslata, deformata per dissesti statici, imprecisioni costruttive, degrado.
Pur con tutte queste limitazioni un edificio è comunque composto per gran parte di solidi regolari o pseudo-regolari.
Il rilievo di un edificio può dunque essere visto come un processo simile alla sua progettazione (vale a dire la unione di una serie finita di componenti modulari elementari ricavati da un abaco), con due essenziali differenze:
- I componenti costitutivi l'architettura reale non sono assimilabili a solidi perfetti, né in tutto e per tutto uguali tra loro.
- La loro posizione nello spazio non è uniformemente distribuita o inquadrabile in una maglia regolare di progetto.

Vengono, in questo campo, in aiuto la topografia e soprattutto la fotogrammetria architettonica rilevando esattamente la forma e la corretta dislocazione degli elementi reali.
I metodi attualmente utilizzati procedono però per saturazione: più è complesso l'elemento da restituire, più punti saranno necessari per una sua definizione esaustiva. Se si pensa a quanti punti si debbono utilizzare per una restituzione a tutto tondo di un solo capitello corinzio, si conosce anche la risposta al perché siano così pochi, ad oggi, i veri modelli solidi di tali edifici.
Da una parte l'acquisizione per via fotogrammetrica di decine di migliaia di punti, dall'altra la loro rielaborazione in contorni e superfici innalzano i costi ben al di sopra del sopportabile.
Del resto anche contando in una ulteriore drastica riduzione dei costi hardware resta pur sempre lo scoglio della digitalizzazione di masse ingenti di punti tridimensionali e la successiva aggregazione in superfici, controllata interattivamente e perciò lenta.
Inoltre resta la tara metodologica che impone la compresenza continua di tutti i punti del modello tridimensionale appiattendo la gerarchizzazione degli elementi e certo non aiutando la loro manipolazione. E va anche tenuto conto che un edificio è composto di elementi solidi più che di superfici che non permettono, ad esempio, un agevole calcolo del volume, del peso o l'interfacciamento con programmi di analisi strutturale per mezzo di elementi finiti.
Infine una tale impostazione non sfrutta che in minima parte (la sola visualizzazione) l'enorme patrimonio di software sviluppato per la progettazione, richiedendo, al contrario, la messa a punto di interi packages ad hoc.



LE DEFORMAZIONI LOCALI

Il metodo proposto, tuttora in fase di studio di fattibilità, propone la suddivisione dei punti di un modello tridimensionale in tre insiemi, quantitativamente di molto inferiori a quanto richiesto tradizionalmente. Riuniti , essi raggiungono una massa critica sufficiente a sviluppare una grande quantità di punti visualizzabili e manipolabili da programmi CAD.
Attraverso un esempio vediamo nel dettaglio lo svolgersi delle fasi. Mediante la modellazione solida risulta agevole costruire una colonna completa anche complessa a partire da poche misure essenziali; inoltre la quantità di punti (che chiameremo genitori) è estremamente ridotta per ulteriori colonne che richiederanno solo i parametri di collocazione: le traslazioni, le rotazioni e le scalature.
Se viene richiesta la visualizzazione dell'intero colonnato, si genera automaticamente un gran numero di punti figli, così come un cerchio può essere individuato come un centro ed un raggio ma rappresentato con dieci, mille o un milione di punti ottenuti dalla sua equazione.
È però evidente che queste colonne ideali saranno vicine ma assolutamente non coincidenti con quelle reali. Le variazioni di queste ultime rispetto alle prime potranno essere puntuali (sbrecciature, fessurazioni, rotture), estese (schiacciamento, torsione) o posizionali (disassamenti, rotazioni).
Sarà perciò necessario deformare ogni singola colonna ideale, sino a minimizzare le differenze con la rispettiva colonna reale. Per ottenere tale risultato si può procedere con le seguenti modalità:

A) Di ogni colonna reale vengono rilevati due insiemi mirati di punti:
- un primo insieme, che definiremo di punti attrattori.
- un secondo, di punti di controllo.
Ognuno di questi punti avrà un suo omologo appartenente alla colonna ideale.

B) Unendo punti attrattori omologhi a partire da quelli sulla colonna ideale verso quelli sulla colonna reale, si otterranno tanti vettori forza quante sono le coppie di punti attrattori. Tali vettori saranno dotati di modulo, versori lungo gli assi e direzione e potranno esercitare la loro forza, funzione della distanza: funzione scelta dall'utente o, come vedremo più avanti, da programma, dotata della caratteristica di tendere all'infinito quando la distanza tende a zero ed a zero se la distanza tende all'infinito. Se ad esempio la funzione è 1/distanza, un punto posto ad una unità dall'attrattore sarà sottoposto ad una forza unitaria, se distante 0.1 unità la forza sarà dieci volte maggiore. Se la distanza è zero (se il punto coincide dunque con un attrattore) la forza sarà infinita e quindi il punto coinciderà con l'estremo finale del vettore forza. Ciò significa che tutti i punti attrattori appartenenti alla colonna ideale coincideranno, dopo la deformazione, con i loro omologhi della colonna reale.
Ogni punto figlio della colonna ideale sarà dunque sottoposto ad un campo di forze che tenderà a spostarlo dalla posizione iniziale. Tanto più un punto figlio si troverà vicino ad un attrattore tanto più sarà influenzato dal destino di questo, dal modulo della forza applicata e dalla sua direzione.

C) Da quanto visto sappiamo che i punti attrattori ideali coincidono, dopo la deformazione, con i loro omologhi reali. Di tutti gli altri punti, i figli, non possiamo controllare la corretta dislocazione a meno di non aver distribuito tra questi un congruo numero di punti di controllo. Un programma modulerà le funzione forza fino a minimizzare, eseguita la deformazione, la differenza ancora esistente tra ogni punto di controllo ideale ed il suo omologo reale. Se il set di punti di controllo è sufficiente in numero e ben distribuito, sarà possibile stabilire statisticamente quando la colonna ideale deformata avrà raggiunto la approssimazione voluta, a meno di uno scarto quadratico medio dato dalla somma degli scarti calcolati tra i punti di controllo reali ed i loro omologhi ideali dopo la deformazione.
È da tenere presente che anche i punti di controllo saranno dotati di un peso che permetterà di distribuire l'errore con le modalità volute dall'utente.



LA SCELTA DELLA FUNZIONE FORZA

Per prima cosa si sono ricercate le funzioni più idonee e controllabili. Le figure che seguono mostrano le assonometrie di cubi deformati con le modalità esposte, utilizzando le seguenti funzioni:

- l'inverso della radice quadrata della distanza;
- l'inverso della distanza;
- l'inverso della distanza al quadrato;
- l'inverso della distanza al cubo;
- l'inverso della distanza alla quarta
- l'inverso dell'esponenziale della radice quadrata della distanza;
- l'inverso dell'esponenziale della distanza;
- l'inverso del logaritmo neperiano della radice quadrata della distanza.

Si nota che la funzione più duttile e stabile risulta essere l'inverso dell'esponenziale della distanza. Inoltre, da un'ulteriore analisi si è notato che elevando la distanza ad un esponente compreso tra zero ed uno si è in grado di modulare ancor più gli effetti della forza sui punti figli.
Aggiungendo infine un peso moltiplicatore, maggiore di zero, e suddividendo gli effetti in X, Y, Z si giunge ad un completo controllo delle deformazioni.

La forma finale della funzione di deformazione sarà dunque:

DEFORMAZIONE(X,Y,Z)=PESO(X,Y,Z)*1/EXP(DISTANZA(X,Y,Z)^A)    (1)

dove ^A è appunto un esponente variabile tra zero ed uno.
Se N è il numero di punti attrattori, ogni punto figlio sarà sottoposto ad un campo generato da M=N*3 (le tre componenti X,Y,Z) forze contrastanti date dall'equazione (1).
Un programma si incaricherà di variare M*2 coefficienti (il peso e l'esponente di ogni equazione) con l'obiettivo di minimizzare lo scarto quadratico medio tra i punti di controllo ideali e quelli reali, dando per scontato che comunque i punti attrattori ideali, dopo la deformazione, coincideranno con quelli reali.



CONCLUSIONI

Nell'articolo viene presentato un metodo per la deformazione di componenti architettonici rilevati. Tale metodo non è orientato alla definizione per saturazione di informazioni, ma tende al raggiungimento dell'obiettivo in due fasi separate:
A) Costruzione, per mezzo della modellazione solida, di componenti ideali simili topologicamente e metricamente ai loro omologhi reali.
B) Deformazione dei componenti ideali per mezzo di punti attrattori fino a minimizzare lo scarto tra questi e i componenti reali rilevati per via topografica o fotogrammetrica. Il controllo della deformazione avviene per mezzo di punti di controllo opportunamente distribuiti sulla superficie dei componenti.
I vantaggi derivanti da tale metodo sono essenzialmente due:
1) La manipolazione dei componenti può essere controllata per buona parte da normali programmi di modellazione solida. Questo consente l'utilizzo di un gran numero di programmi esistenti molto sofisticati oltre a tecniche di modellazione sedimentate, proprie della progettazione assistita da elaboratore (CAD).
2) La maggiore complessità dovuta per la fase di deformazione dei componenti è comunque di gran lunga meno pesante, in termini di punti digitalizzati, rispetto ad un approccio esaustivo. Inoltre è possibile modulare la precisione e l'accuratezza aumentando a piacere il numero dei punti di controllo e degli attrattori.
Ad esempio, nel caso si voglia semplicemente rappresentare in assonometria o prospettiva l'intero edificio le deformazioni saranno ridotte al minimo; se, al contrario, si rende necessario uno studio puntuale e preciso di una parte dell'edificio si aumenterà la precisione anche fino a raggiungere quella tipica di un modello esaustivo.
Al momento attuale si sono messi a punto due programmi, ancora allo stadio di prototipi, scritti in linguaggio Pascal, operativi su sistemi Windows. Il primo visualizza in modo interattivo le deformazioni di un solido elementare, come ad esempio il prisma. Il secondo ricerca per successive iterazioni il minimo scarto tra un componente ideale deformato ed il suo omologo reale.
Inoltre un algoritmo del tutto analogo è implementato anche nel programma didattico Cartesio.

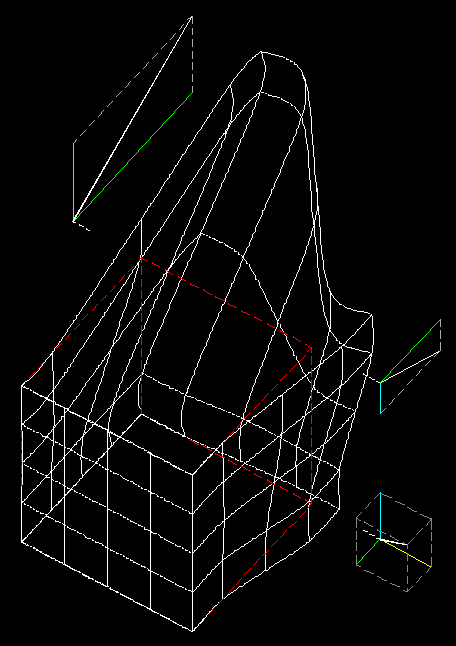Assonometria del cubo deformato in funzione dell'esponenziale della distanza. Il cubo è stato suddiviso in parti per evidenziare gli andamenti di deformazione: risulta evidente che le parti più distanti dai "vettori forza" non vengono influenzate da questi ultimi. Ai lati del cubo sono evidenziati i tre "vettori forza" con le relative componenti: due vettori sono caratterizzati da due sole componenti, il terzo da tre distinte componenti in X, Y e Z. In colore rosso e in linea tratteggiata è mostrato invece il cubo di partenza. Come si può vedere più avanti, negli altri casi - usando altre "funzioni forza" - emergono alcune deformazioni "fantasma", applicate su punti non previsti della faccia anteriore del cubo.

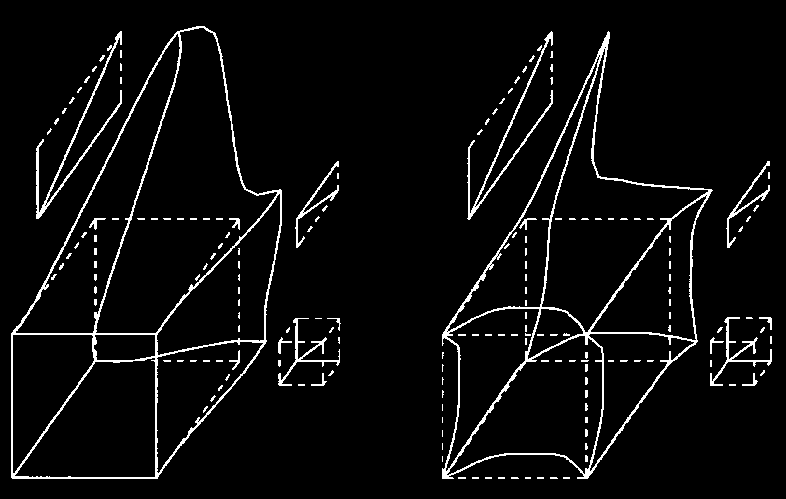Figura a sinistra - Cubo deformato in funzione di EXP distanza (come per la prima immagine). Figura a destra - Cubo deformato in funzione del logaritmo della radice quadrata della distanza.

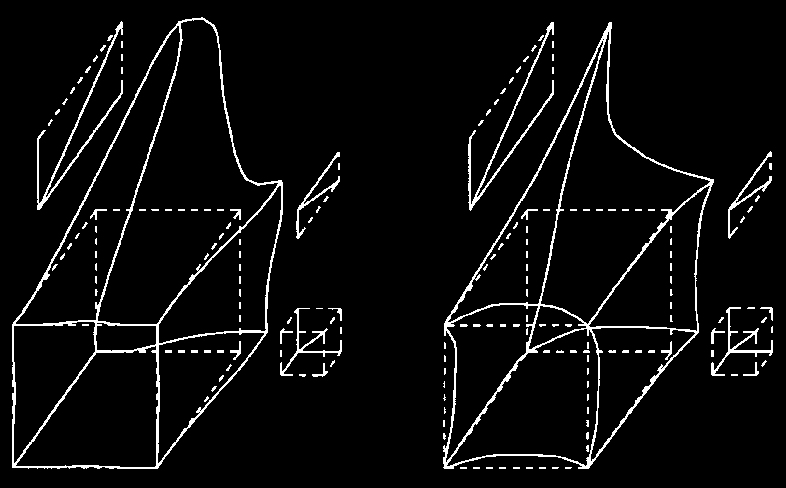Figura a sinistra - Cubo deformato in funzione della distanza alla quarta. Figura a destra - Cubo deformato in funzione di EXP radice quadrata della distanza.

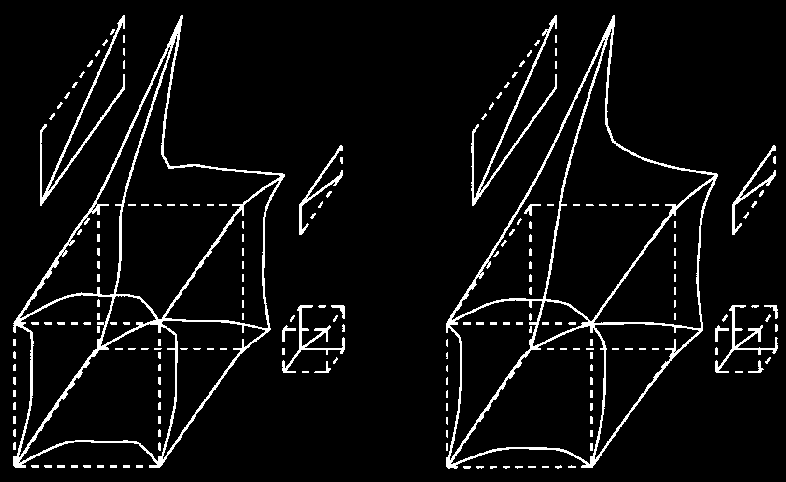Figura a sinistra - Cubo deformato in funzione della radice quadrata della distanza. Figura a destra - Cubo deformato in funzione della distanza.

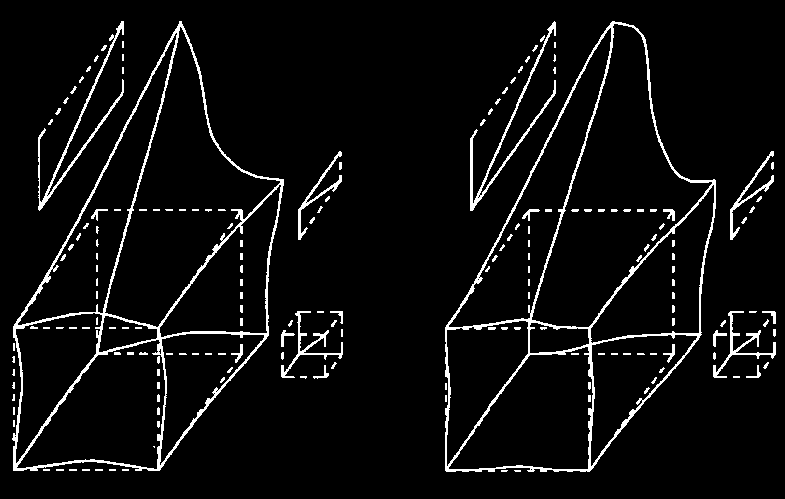Figura a sinistra - Cubo deformato in funzione del quadrato della distanza. Figura a destra - Cubo deformato in funzione del cubo della distanza.

APPENDICE

Di seguito vengono presentate alcune funzioni utilizzate nei programmi.

function forza(dist,espon:real):real;
begin
   dist:=dist*coef_rid;
   if dist<epsi then forza:=max_forza else
      forza:=1/exp(elev(dist,espon));
end;

I significati delle variabili o costanti in neretto sono:

dist	distanza in X, Y o Z del punto figlio considerato dal punto attrattore considerato
espon	esponente A
coef_rid	coefficiente di riduzione che permette di contenere l'oggetto in un cubo di lato 10 unità
epsi	costante piccola a piacere per stabilire quando la distanza è da considerarsi a zero
max_forza	costante grande a piacere per indicare forza infinita
elev	funzione di elevazione: distespon

function delta(tipo:integer;coord,peso,espon:real):real;
var term,term1,d :real;
    k            :integer;
begin
    term1:=0;d:=0;
    for k:=1 to punti_att do
          begin
       term:=peso*forza(abs(coord-p_att[k,tipo]),espon);
       term1:=term1+term;
                d:=d+diff[k,tipo]*term;)
    end;
    delta:=d/term1;
end;

I significati delle variabili in neretto sono:

tipo	indica la coordinata X, Y o Z
coord	coordinata X, Y o Z del punto figlio considerato
punti_att	numero totale di punti attrattori
peso	peso assegnato ad una coordinata di un punto attrattore
espon	esponente A
p_att	matrice contenente le coordinate dei punti attrattori
diff	matrice contenente i moduli delle forze in X, Y, Z

BIBLIOGRAFIA

A.A.V.V., Dispense del corso Computational Geometry: Modellazione geometrica e superfici sculturate, Politecnico di Milano, 1986.
A. Puppo, Prontuario e formulario di matematica, Patron, 1982.
I.D. Faux M.J. Pratt, Computational geometry for design and manufacture, Ellis Horwood, 1979.
D.H.McLain, Drawing contours from arbitrary data points, in "The Computer Journal", Vol. 17, N. 4.
T.A. Foley, Weighted bicubic spline interpolation to rapidly varying data, ACM Transactions on Graphics, Vol. 6, N. 1.
F. Cheng A. Goshtasby, A parallel B-splines surface fitting algorithm, ACM Transactions on Graphics, Vol. 8, N. 1.
P.J. Davis, Interpolation and approximation, Blaisdele, 1963.

o