
Analisi
e comparazione dei software di Reverse Modeling
in commercio
a cura di Massimiliano Ciammaichella
Il
Reverse Modeling, metodologia di progettazione indispensabile per il
raggiungimento in tempi estremamente rapidi di risultati ad altissimo contenuto
qualitativo, si identifica nella riproduzione grafica tridimensionale del dato
materiale per mezzo del rilievo, al fine di ricostruire un prototipo fisico dell’oggetto.
La
contemporaneità implica un’inversione di tendenza: il rilievo anticipa il
progetto quale mezzo di introspezione e restituzione grafica del dato materiale.
La
scansione laser 3d risulta essere un ottimo strumento per l’acquisizione di
dati numerici che mimano la forma dell’oggetto reale per mezzo di nuvole di
punti e/o superfici Mesh[1]:
poliedri, modelli numerici utili alla costruzione di un modello matematico, che
indaghi la genesi geometrica e pertanto ripercorra le tappe
tettonico-compositive del progettista.
La
dicitura Reverse Engineering, invece, si riferisce alla progettazione inversa, ossia
alla progettazione e allo sviluppo di un prototipo che si avvale di un modello tridimensionale ottenuto
dalla digitalizzazione di un tipo fisico.
Tre sono le fasi del processo di Reverse Engineering:
-
acquisizione
del modello numerico,
- conversione dello stesso in modello matematico (CAD),
-
ricostruzione
di un prototipo fisico (CAM).
Il
modello numerico si manifesta in una nuvola di punti che verranno
successivamente uniti per formare una superficie Mesh, ossia una maglia
poligonale, vero e proprio poliedro a facce orientate.
Per
conversione del modello numerico in modello matematico si intende invece la
creazione delle superfici geometriche, NURBS[2],
che descrivono l’oggetto punto a punto, per via di equazioni parametriche.
Questo
processo: che inizia dal rilievo, e quindi dall’acquisizione del modello
numerico dell’oggetto, e che termina in un modello matematico, prende il nome
di Reverse Modeling.
Esistono
poi degli strumenti (CAM) che permettono, attraverso sistemi meccanici, di
produrre il prototipo materiale dell’ente rilevato.
In
questo caso tuttavia si dovrà parlare di Reverse Engineering.
Dall’oggetto
finito si passa alla sua rappresentazione.
In
prima analisi si ottiene un modello numerico, una nuvola di punti ricavati dal
rilievo, con sistemi di tipo: meccanico, digitale, ibrido.
I
sistemi di rilevazione basati su procedimenti meccanici adottano sonde, guidate
dal movimento manuale attorno all’oggetto di indagine. I sensori
elettro-ottici, o elettromagnetici, montati sulla sonda, forniscono le
informazioni relative alla posizione dell’oggetto per mezzo di un software di
acquisizione di dati numerici.
Le
incertezze su tale metodologia nascono dalla considerazione che le sonde sono a
diretto contatto con l’oggetto, così le superfici da rilevare possono subire
storture, compromettendo il modello finale.
Altre
incongruenze possono verificarsi nella cattura di superfici multicolore.
I
sistemi di rilevazione meccanica, tuttavia, sono indicabili per la riproduzione
delle superfici in prossimità di bordi spigolosi, e non risentono dei problemi
di cattura dello spazio al contesto che hanno i sistemi basati su camere
digitali senza contatto fisico.
Sistemi digitali, quali i Laser Scanner, sfruttano due metodologie di misurazione:
-triangolazione ottica: per scansioni ad elevata risoluzione di oggetti di piccole dimensioni, posizionati ad una distanza molto ridotta (0,5:25m) dallo scanner;
-tempo
di volo: per oggetti di grandi dimensioni, quali edifici, disposti a distanze
elevate rispetto allo scanner (2:150m).
La triangolazione laser è un processo stereoscopico attivo, in cui la distanza della macchina dall’oggetto d’indagine è automaticamente computata per mezzo di una fonte di luce direzionale e un video: il fascio laser emesso viene deviato da uno specchio sull’ente da esaminare. L’immagine è simultaneamente raccolta da un video che ne calcola la distanza.
Applicando poi la trigonometria alle coordinate spaziali, 3D, un punto (x,y,z)
viene automaticamente calcolato e memorizzato in un archivio che può essere
inserito in un software di gestione dei dati.
Il
sistema seleziona i profili dell’oggetto direttamente sulla superficie, compie
cioè una sorta di allineamento “2D”, fornendo valori numerici a tutti i
punti in esame lungo il fascio laser (fig. 01).

01- Triangolazione Laser
Questo
tipo di tecnologia al laser, senza contatto fisico, consente di rilevare
materiali complessi come l’argilla, la gomma…, ed è particolarmente adatto
alle superfici contrassegnate da una certa complessità geometrica.
In
realtà tutti i sistemi che forniscono valori numerici da scansione laser
tridimensionale utilizzano tecnologie basate sulla triangolazione.
L’apparecchiatura è provvista di una doppia camera fotografica.
Una
sonda emette un fascio di luce laser da un diodo centrale. Il fascio è diviso
da un piano di luce laser, emesso dalla sonda, che colpisce la superficie
dell’oggetto. Così si genera un profilo sull’area analizzata.
Il
profilo bidimensionale è registrato dalla camera digitale. La sua posizione Z
è determinata e memorizzata per ogni valore, del pixel, dal software.
Questa
posizione, con la collocazione degli assi della macchina, è necessaria alla
computazione delle coordinate X, Y, del profilo. Le centinaia e le migliaia di
sagome simili vengono sondate contemporaneamente.
Gli
odierni software memorizzano queste informazioni in una base di dati.
Ogni profilo rientra nella memorizzazione come singola entità, polilinea.
Queste
“polyline” sono visualizzate graficamente sullo schermo del calcolatore
mentre vengono raccolte.
Nella
metodologia del “tempo di volo” (TOF)[3],
fasci di luce laser a più impulsi colpiscono il bersaglio da rilevare. Parte
dell’energia emessa viene riflessa dall’oggetto e ritrasmessa alla macchina
che valuta le coordinate dei punti scansiti in termini di distanza, in virtù
del tempo impiegato dalla sorgente (scanner 3d) per emettere un fascio di luce
laser, bersagliare l’oggetto (target), e riflettere il raggio allo scanner.
Esistono
poi sistemi di misurazione ibridi che sfruttano i pregi di entrambe le
metodologie. Alcuni Scanner Laser, (Minolta), assieme al rilievo geometrico
comprendono quello del colore, eliminando gli errori dovuti ai fenomeni di
ombreggiamento.
I
sistemi meccanici a contatto fisico allo stesso tempo consentono una
riproduzione, molto prossima all’esattezza, di dati numerici relativi alla
geometria di superfici con angoli acuti.
Le
metodologie di rilievo indicate presuppongono l’esistenza fisica del dato
materiale, la forma è analizzata attraverso strumenti differenti: Robot
palpatori, o Laser Scanner.
Si
ricorda che il modello risultato delle operazioni è sempre una nuvola di punti,
un modello numerico, punti uniti da rette a formare aree triangolari o
quadrangolari, poliedri.
La
geometria dell’ente non è ancora stata esplorata. Quali sono gli algoritmi
utili alla conoscenza delle sue superfici? Come si può comprendere il modello
matematico, analitico, di superfici che rivestono una massa?
I
comuni modellatori solidi offrono la possibilità di costruire facilmente
modelli matematici, sulla scorta di modelli numerici risultanti dalle operazioni
di rilevamento digitale, da Scanner Laser 3D o da “robot palpatore”.
Costruita
la nuvola di punti, si devono rappresentare le superfici che rivestono
l’oggetto.
I punti rilevati diverranno i vertici di facce piane, triangolari o quadrangolari…
Esistono differenti algoritmi di generazione di Superfici Mesh
a partire da nuvole di punti. Il più comune si basa sulla
Triangolazione del matematico francese Delaunay[4]
(fig. 02).
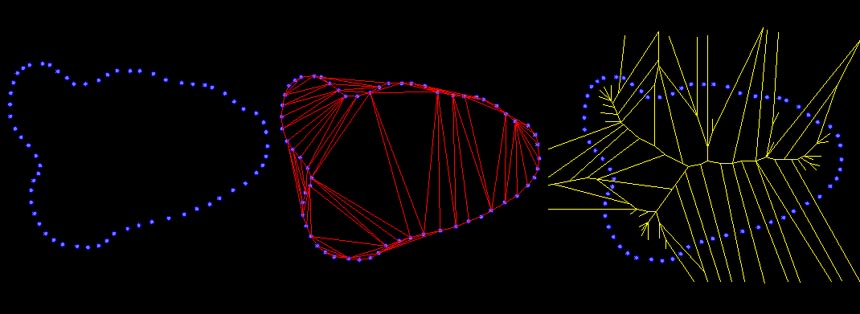
02- Punti, Triangolazione di Delaunay, Celle di Voronoi
L’algoritmo
di Delaunay definisce una rappresentazione grafica di possibili connessioni fra
punti dello spazio in gruppi di tre o quattro. I gruppi di tre punti generano i
Triangoli di Delaunay, i gruppi di quattro creano i tetraedri di Delaunay, che
possono essere sempre ricondotti a dei triangoli.
Per definire la triangolazione di Delaunay è necessario riconoscere il significato di diagramma di Voronoi. Un diagramma di Voronoi è la rappresentazione delle relazioni di vicinato di n punti nello spazio bidimensionale o tridimensionale.
Sia S un insieme finito di n punti nel piano. Per ogni punto PäS possiamo definire, come Poligono di Voronoi, quell’insieme di punti del piano più vicini a P rispetto ad ogni altro punto dell’insieme S. L’insieme di tutti i poligoni di Voronoi, dell’insieme di punti S, prende il nome di Diagramma di Voronoi. La triangolazione di Delaunay è costruita connettendo i punti PäS tra loro, se e solo se i loro poligoni di Voronoi hanno un lato in comune…
Sono
riportati: (fig. 3) in blu i triangoli di Delaunay, in rosso le regioni di Voronoi.
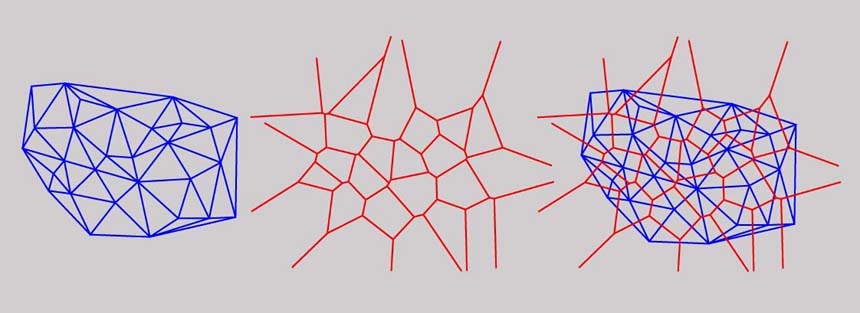
03- Triangoli di Delaunay, Celle di Voronoi
Le
superfici poligonali approssimano le forme curve dell’oggetto rilevato attraverso la rappresentazione di un poliedro a facce orientate.
Il
rilievo qui è identificato nella ricostruzione del progetto attraverso la
definizione di un modello matematico, a partire da una nuvola di punti e/o da
una superficie Mesh già predisposta.
A
partire da quest’ultima premessa verranno ora analizzate le caratteristiche
degli odierni software di Reverse Modeling atte alla messa in essere di un
modello geometrico tridimensionale. Queste sono le principali fasi di indagine: post
processing, trattamento delle nuvole di punti già unite in un modello
numerico (merging), decimazione di punti, algoritmi di smoothing; creazione di curve caratteristiche sul modello numerico Mesh;
generazione di superfici matematiche; algoritmi di comparazione del modello
matematico con il modello numerico, analisi degli scarti e deviazioni standard.
Post
Processing
Algoritmi
di decimazione della Nuvola di punti
Generalmente
i software utilizzano l’algoritmo di Garland e Heckbert[5]
per ridurre il numero di punti in un modello numerico unito. La
decimazione di Garland ed Heckbert unisce punti approssimativamente complanari.
Tutti i punti che approssimano la superficie piana vengono eliminati, tranne
quelli che definiscono la geometria di bordo della regione piana.
L’eliminazione
dei poligoni da una Mesh è il processo che riduce il numero di primitive
geometriche in un modello 3d, minimizzando le differenze fra modello numerico di
partenza e finale.
-Polyworks v.8.0 (innovmetric)- assicura il mantenimento di importanti caratteristiche geometriche in fase di decimazione: preservazione della topologia locale nelle superfici, degli spigoli fra superfici, mappaggio dei vertici della Mesh del modello originale sul modello ridotto, calcolo della massima distanza fra vertici in funzione di un livello di tolleranza preimpostato.
Quando due gruppi di poligoni
sono adiacenti il modulo IMCompress legge gli spigoli formati dai due
gruppi, le aree confinanti sono ridotte, ma viene mantenuta la topologia.
Il
software crea una mappa degli errori fra modello di partenza e ridotto.
Il
modello di colore RGB viene utilizzato per mostrare i discostamenti fra vertici
originali e ridotti. Il blu corrisponde ad una tolleranza negativa, il verde
rappresenta lo zero, il rosso mostra un livello di tolleranza ottimale.
Il
modulo IMEdit possiede un algoritmo di filtraggio di punti della nuvola,
servendosi di una sfera rotante (rolling-ball).
Si
può fissare il raggio della sfera che meglio approssima la mesh, verificando se
sono presenti vertici non raggiunti dalla sfera interpolante. Se ciò accade,
significa che localmente la curvatura della superficie stimata è più elevata
del raggio di curvatura della sfera. Il comando sposta i vertici più lontani
fino a farli coincidere con la superficie sferica. Questa opzione è utile per
specificare la massima curvatura di una superficie e può applicarsi alla mesh
nella sua totalità o localmente.
-RapidForm
2004 PP1 (INUS Technology)- Si può ridurre il numero di poligoni della
mesh
diminuendo il dettaglio della superficie originale. In aree dove non si
necessita di mantenere un elevato numero di punti: regioni piane o non rugose,
si può applicare la decimazione preservando la forma della superficie
originale. Si possono decimare superfici multiple nello stesso tempo.
L’operazione
prevede 3 opzioni: numero di facce, rapporto di riduzione, e errore limite.
La
decimazione si può applicare a tutto il poliedro o selettivamente.
-3D
RESHAPER (technodigit)- Si selezionano regioni contenenti punti da
eliminare, o la nuvola nella sua totalità. Tutti i punti lontani dalla nuvola,
che non rientrano nel livello di tolleranza scelto, vengono scartati. Nella fase di eliminazione viene ricreata la superficie
mesh
con la possibilità di ridurre il rumore, con un range di spostamento dei
vertici impostato.
Il software costruisce circonferenze, sfere, e piani che approssimano nel modo migliore la geometria della Mesh. Dal confronto è possibile visualizzare la deviazione standard fra enti geometrici. I punti di massimo scostamento verranno segnalati con un cambio di colore, e la possibilità di eliminarli (fig. 04)
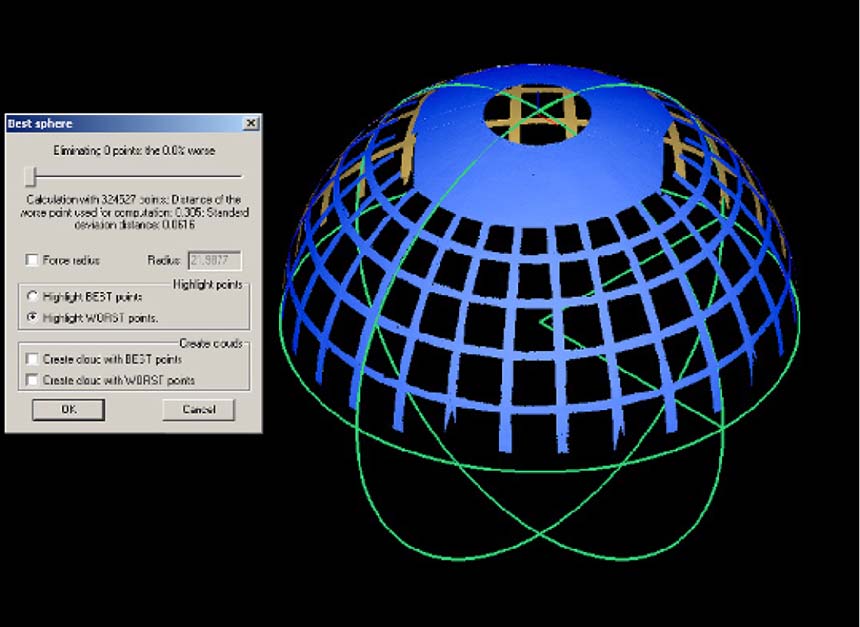
04- Modello numerico della Cupola del Pantheon. La Mesh è interpolata da una sfera di raggio 21,9877 (circa 148 piedi romani, con piede= 29,71cm), la deviazione standard è pari a 6,16 cm. Le nuvole di punti sono state acquisite dal professor Riccardo Migliari, con Scanner Laser Cyrax 2500, nel gennaio 2002
-SLIM3D
(3d Shape GmbH)- dispone di diversi algoritmi per filtrare punti.
Filtri
come il mediano, e il gaussiano, agiscono soltanto lungo la coordinata z,
andando a ridurre l’eventuale rumore della nuvola.
Un buon filtro 3d, presente nel software, è quello che permette di eliminare punti non significativi che appartengono a regioni riconoscibili in superfici note come i piani e i cilindri.
Si stimano le differenti curvature del modello numerico che sono graficizzate con colori: il rosso corrisponde ad una distribuzione di punti ascrivibili al piano, il verde identifica una superficie cilindrica convessa, il blu una superficie cilindrica concava, il giallo una superficie generica concava, il ciano una superficie a doppia curvatura come le selle.
Ogni filtro
di decimazione può causare un’errata ridistribuzione dei punti,
compromettendo una corretta ricostruzione della superficie mesh. Si può
ottimizzare la geometria del modello numerico spostando i vertici e assicurando
il mantenimento della curvatura delle superfici, omogeneizzando la dimensione dei triangoli.
-SURFACESTUDIO
11 (Alias Wavefront)- elimina punti in regioni non significative
confrontando il modello numerico con superfici NURBS create dall’utente.
-Paraform
(Metris)- riduce i punti attraverso l’analisi della curvatura delle
superfici che compongono la mesh, la misurazione avviene servendosi di una
griglia proiettata sul modello. Si possono costruire delle superfici Nurbs
che approssimano le regioni di nuvola, misurare i discostamenti ed eliminare dei
punti dal modello numerico.
-PowerSHAPE
5.5.41 (Delcam)- La decimazione della nuvola di punti avviene selettivamente
o nel modello totale, con primitive geometriche quali: sfera, cilindro, cubo.
-Geomagic Studio1.0 (RaindropGeomagic)- Possiede una algoritmo di decimazione automatica di punti, stimando preventivamente la curvatura delle superfici, in aree scelte dall’utente o complessivamente su tutto il modello numerico.
Riduce il rumore eventuale stimando le coordinate dei punti nello spazio 3d in
virtù della posizione dei punti vicini. La decimazione può avvenire anche con
superfici: cilindriche, piane, e sferiche.
-RealWorks
Survey V4.1 (Mensi)- Se la scansione laser è prodotta da questo software,
la nuvola di punti è composta di tanti profili allineati su piani paralleli. La
decimazione ispeziona le
diverse curvature del modello e riduce punti superflui appartenenti ai profili di
punti.
-Matchgraph-
È garantita la decimazione sia selettiva che totale, analizzando le coordinate
spaziali dei punti, si può visualizzare una mappa in scala di colore contenente
le differenti curvature del modello numerico.
-Polyworks-
In IMEdit si offrono differenti possibilità per ottimizzare la forma
delle mesh, in virtù della curvatura che si vuole associare alle
superfici.
I
parametri di smoothing definiscono: il numero di iterazioni, il valore del
raggio che specifica la distanza 3d attorno alla quale un vertice può essere
spostato, un valore elevato del raggio aumenta l’effetto di smoothing,
riducendo di molto il rumore.
L’algoritmo
può anche applicarsi su un’area definita: rettangolare o ellittica, così
come si può muovere la posizione di alcuni vertici. Le direzioni di spostamento
sono definite dai vettori normali alle facce.
-RapidForm-
Il processo di smoothing unisce ogni regione curva di poligoni con stessa
curvatura. Si possono variare le coordinate dei vertici aumentando la levigature
delle superfici con un fattore di tolleranza scelto.
Lo
smoothing può utilizzare un pennello per smussare la mesh localmente.
-3D
RESHAPER- Si può aumentare il numero di vertici, creandone di nuovi, nel
processo di levigatura della Mesh. I nuovi punti verranno inseriti nel
poliedro, in quelle zone dove la densità dei vertici non è sufficiente a
garantire una discreta omogeneità di triangoli.
la riorganizzazione dei punti è associata alla
stima delle diverse curvature superficiali che il modello può presentare. Il software
costruisce nuovi triangoli mantenendo inalterata la curvatura anche nelle zone
dove sono presenti incuneamenti o picchi, minimizzando gli errori.
-SLIM3D-
Il primo filtraggio è dato lungo le normali alle facce piane della Mesh,
utilizzando un filtro geometrico non lineare che adatta il riposizionamento dei
vertici al fine di ricreare nuove facce triangolari.
Il
filtro di smoothing adotta anche un approccio geometrico più raffinato:
se ci sono variazioni di curvatura sulle superfici, si associano archi di
circonferenza lungo i profili della nuvola, misurando le variazioni. Lo
smoothing avverrà minimizzando le mutazioni di curvatura.
-SURFACESTUDIO-
costruisce una superficie matematica patch direttamente sulla nuvola
visualizzando le deviazioni, la curvatura, e il discostamento.
I
punti possono essere spostati in virtù di eventuali rumori,
-Paraform-
Il processo di smoothing è elementare e permette di omogeneizzare la
nuvola soprattutto quando è presente del rumore. Funziona localmente e
globalmente.
-PowerSHAPE-
L’analisi della curvatura delle superfici, consente di variare la geometria
della nuvola di punti, ritoccando selettivamente il rumore, e ricostruendo la
mesh in pochi passi. La smussatura può avvenire attraverso un pennello di
selezione che raffina i triangoli stimando la media delle curvature dei
triangoli limitrofi.
-Geomagic
Studio1.0- lo smoothing è automatico, e può avvenire stimando
le curvature superficiali senza alterarle.
-RealWorks-
Se le scansioni sono effettuate con Realworks non è necessario lo smoothing,
poiché tutti i punti vengono distribuiti lungo profili 2d.
-Matchgraph-
analizza la curvatura delle superfici graficizzando la nuvola di punti in scala di
colore. Il processo di smoothing è automatico.
Dal
modello numerico al modello Matematico
Algoritmi
di rappresentazione di curve caratteristiche su modello numerico
La
sezione piana di una superficie Mesh dovrebbe produrre un’entità geometrica
riconoscibile nella polilinea, pur tuttavia i diversi software testati
convertono i vertici in punti di interpolazione per la
rappresentazione di curve.
Dal
modello numerico si passa facilmente alla costruzione del modello matematico
attraverso curve di Bézier[6]
o Nurbs.
-Polyworks-
IMEdit genera curve sezione di modelli poligonali.
Si
tratta di entità geometriche definite dall’intersezioni di piani con
poligoni.
Esistono
più possibilità di generazione di curve: sezioni lungo l’asse x, y, o z.
Si
definisce il numero di piani paralleli di sezione, e quindi il numero di curve
da produrre, o il passo fra le curve, permettendo di chiuderle laddove sono
presenti buchi nella mesh. Le curve possono essere estratte anche da sezioni
radiali: l’intersezione fra due piani definisce l’asse di rotazione. Anche
qui si può impostare il numero di curve da generare e il passo.
Si
producono curve sezione da piani perpendicolari ad una traiettoria curva.
Generate le sezioni bisogna convertire le stesse in curve di Bézier. Si
possono anche creare selettivamente delle curve, direttamente sulla mesh,
editandole dai vertici della mesh che saranno presi come punti di interpolazione
della curva. IMEdit stima la curva teorica dalle superfici più vicine,
alla destra e alla sinistra della curva stessa, definendo distanze minime e
massime dalle superfici, in modo tale da rappresentare la migliore
approssimazione dell’ente geometrico.
Ciò
si attua selezionando un gruppo di triangoli contigui, la migliore
approssimazione matematica del profilo sarà offerta da una curva di Bézier, i
cui punti di controllo saranno individuati nei vertici delle facce triangolari,
e le tangenti saranno rette contenute nei piani dei triangoli (fig. 05).
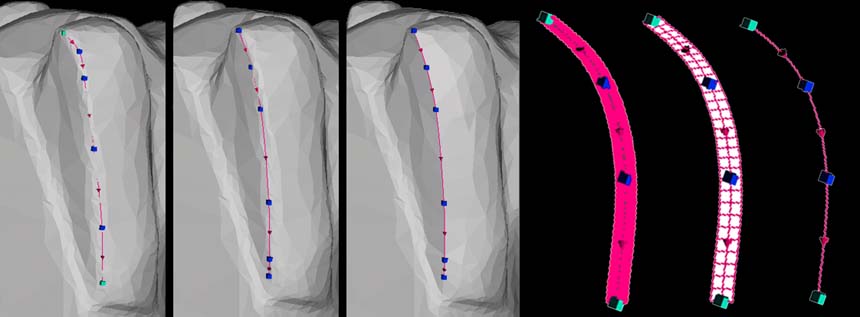
05- Ricostruzione delle curve di Bézier dalla sezione di una Superficie Mesh
-RapidForm-
crea una rete di curve estraendole automaticamente e definendo il numero di
triangoli da interpolare. Anche RapidForm è in grado di tracciare curve
sezione. I bordi della mesh possono essere convertiti in curve Spline, e
si possono disegnare curve libere selezionando un certo numero di punti della
nuvola.
Si
possono proiettare: curve, polilinee, rettangoli, circonferenze, ellissi, e
griglie, direttamente sul poliedro.
E’
assicurata la coincidenza degli enti geometrici in punti noti, e la tangenza, al
fine di produrre un network di curve utili alla rappresentazione di
superfici matematiche.
-3D
RESHAPER-
produce Sezioni piane ed estrae curve nelle regioni di bordo della mesh, dove la
variazione di curvatura fra le facce piane è notevole (fig. 06).
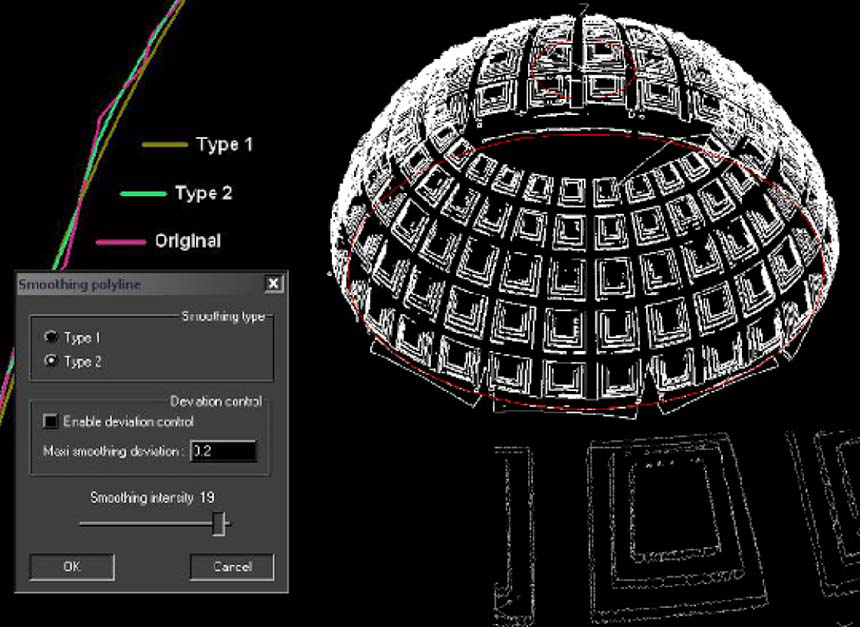
06-Cupola del Pantheon, Estrazione delle curve di bordo
-SLIM3D-
Costruisce curve sezione
-SURFACESTUDIO-
traccia: curve sezione, curve libere sulla Mesh, e curve di bordo. Gli
enti geometrici vanno poi convertiti, da polilinee, in curve NURBS.
-Paraform-
Produce curve sezione come gli altri software analizzati, ma anche curve spline
su modello numerico servendosi dei punti della nuvola come punti di
interpolazione.
-PowerSHAPE-
Crea curve su modello numerico, sia per sezione che per estrazione di bordi. Si
possono tracciare curve caratteristiche da punti estratti come tracce di profili
possibili.
-Geomagic
Studio- crea curve sezione.
-RealWorks- produce curve sezione e curve di bordo.
-Matchgraph-
crea curve sezione e curve Nurbs libere, tracciate direttamente sulla Mesh.
Algoritmi
di generazione di superfici matematiche su modello numerico
-Polyworks-
IMEdit permette di convertire il modello numerico in superfici Patch[7]
secondo 2
modalità: le patch si adattano alle regioni rettangolari del poliedro, e
si possono anche generare patch cilindriche.
-RapidForm-
costruisce superfici patch direttamente sulla nuvola di punti e non solo:
generate le curve, con gli algoritmi già visti, si rappresentano superfici patch
determinandone il numero di generatrici e direttrici (u,v), a seconda della
complessità formale. Le differenti superfici saranno unite in un solo modello
matematico, assicurando la continuità.
Si
tracciano: superfici di traslazione, di rivoluzione, superfici skinned,
superfici swept.
-3D
RESHAPER-
Non previsto.
-SLIM3D-
Non previsto.
-SURFACESTUDIO-
Costruisce superfici patch, e tutte le Nurbs avanzate,
consentendone la modifica per spostamento di punti di controllo e assicurando la
tangenza e la curvatura fra superfici di raccordo.
-Paraform-
si costruiscono superfici patch dalle curve preventivamente generate, ma
anche le superfici Nurbs più avanzate: di rivoluzione, di traslazione, swept,
skinned. Le stesse superfici possono poi essere ritoccate nei punti di
controllo attraverso algoritmi di unione delle superfici, e di raccordo.
-PowerSHAPE-
Costruisce superfici freeform, patch, direttamente sulla nuvola.
-Geomagic
Studio-
è in grado di rappresentare patch, e superfici swept multiple.
-RealWorks Survey- Non previsto.
-MATCHGRAPH-
costruisce superfici patch.
Algoritmi
di comparazione del Modello Numerico con Il Modello Matematico
Alcuni dei software qui testati permettono di verificare l'aderenza fra modello matematico e numerico.
Le nuvole di punti possono essere convertite in superfici patch, oppure parti del modello numerico vengono riconosciute nella geometria di solidi platonici quali sfere o cilindri.
Si definisce un asse di rotazione o di estrusione per il profilo da interpolare... La superficie cilindrica, la sfera, o il piano, possono essere confrontati con la geometria della nuvola di punti, alla ricerca di eventuali discostamenti. Le deviazioni standard, gli scarti fra modelli, sono visualizzati in scala di colore.
Il software Scanner3D considera la nuvola di punti nella sua totalità, o parte di essa, come essere la rappresentazione numerica di un solido generato: per traslazione di un profilo lungo una traiettoria rettilinea, o per rotazione di una sezione piana attorno ad un asse complanare.
Si carica la mesh, o la nuvola di punti, in Autocad.
Attivando il comando "Leggo File" il software richiede di specificare se il solido ideale è generato da rotazione o da traslazione. Si inseriscono le coordinate di due punti che identificheranno la retta direttrice, e infine verrà creato un file in formato DXF contenente i punti rototraslati, tutti allineati sullo stesso piano sezione.
L’algoritmo elimina i punti sovrapposti e consente all’utente di tracciare il profilo per segmenti, o curve tracciate da archi di circonferenza.
Si può verificare lo scarto quadratico medio delle distanze tra i punti della nuvola e il solido ideale, generato dal profilo di sezione. Basta attivare il comando "Scarti", indicare il file da elaborare, contenente la nuvola di punti, e il nome del file contenente il profilo di sezione. Si definisce il numero di falsi colori da associare al file grafico contenente indicazioni sugli scarti.
Il programma esegue una serie iterativa di verifiche tendenti a ridurre al minimo lo scarto quadratico medio delle distanze fra i punti della nuvola e la superficie generata dal profilo di sezione, ciò in virtù di un coefficiente di miglioramento indicato dall’utente (è consigliabile un valore pari a 0,000001), (fig. 07). Attivando il comando "Proporzioni" si può attuare il calcolo dei rapporti e delle proporzioni fra le misure della sezione generatrice.
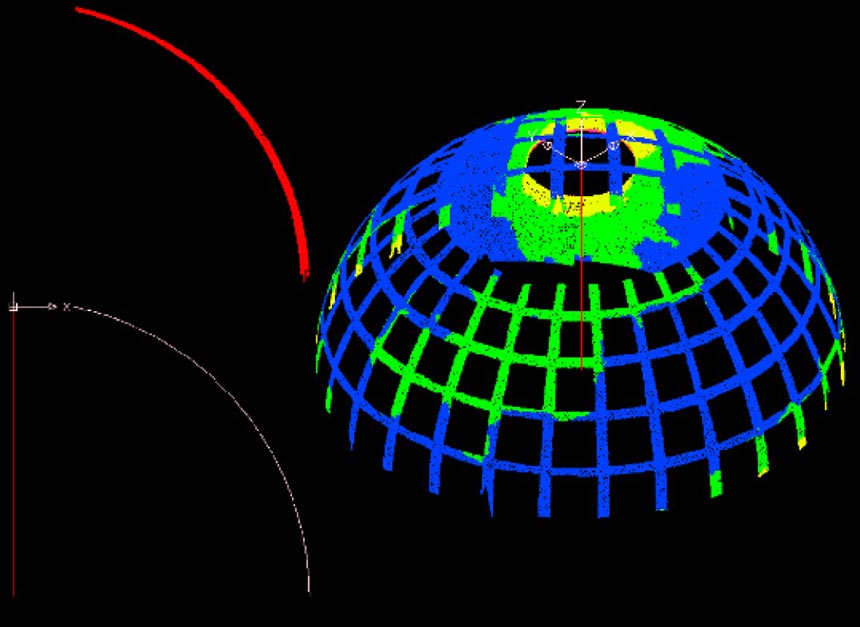
07-Cupola del Pantheon, Costruzione del Profilo e Analisi degli scarti
-Polyworks-
Il modulo IMInspect crea le
primitive più aderenti alla forma del modello numerico di indagine:
Circonferenze, Cilindri, sfere, piani, punti e vettori.
Si
selezionano parti della mesh che meglio approssimano la figura geometrica
scelta. IMInspect restituisce i valori minimi e massimi di
approssimazione secondo tolleranze. Il software scarta punti al di fuori del
valore impostato, adattando l’ente geometrico ai punti testati.
Si
definisce anche il massimo angolo fra i vettori normali ai punti considerati e
il vettore normale alla primitiva scelta. L’algoritmo si usa per ottenere la
massima aderenza fra primitiva e mesh.
Nella
finestra relativa alle proprietà delle primitive si trova una tabella
dell’adattamento statistico con il numero di punti utilizzati nella
computazione e la deviazione standard.
-RapidForm-
permette di costruire il modello matematico direttamente sulla nuvola di punti, estraendo
superfici patch, si opera
l’analisi della deviazione standard fra nuvola di punti e modello matematico.
L’allineamento fra i modelli avvenire in maniera automatica, selezionando
punti omologhi dei modelli.
L’analisi
dei discostamenti mostra la deviazione standard in coordinate x,y,z delle
porzioni di superficie scelta, e un grafico in scala di colore mostra le
deviazioni del modello nella sua totalità riportando anche, in foglio
elettronico, le deviazioni massime e minime. L’analisi delle deviazioni può
avvenire localmente selezionando un gruppo di poligoni della mesh, e curve sezione.
-3D
RESHAPER- Non presente
-SLIM3D-
Generate le curve sezione il software permette di visualizzare in rgb le
deviazioni standard tra superficie mesh e curve caratteristiche, nelle aree in
cui tali curve sono disposte.
-SURFACESTUDIO-
Analizza le curvature del modello
numerico confrontandole con curve caratteristiche estratte. Stima le deviazioni fra
modelli numerici e superfici matematiche. Le deviazioni sono mostrate in scala
di colore e un rapporto con tutti i valori stimati viene prodotto
automaticamente.
-Paraform-
Compara le curve sezione, o curve generiche, con il modello numerico, gli
errori vengono mostrati in rgb direttamente sulle curve e viene generato
automaticamente un rapporto con indicate le deviazioni standard.
-PowerSHAPE-
l’analisi dei discostamenti avviene sia con curve che con superfici
matematiche da confrontare con la Mesh. Anche qui viene visualizzata la
deviazione standard in scala di colore, di ciascun punto della nuvola, dalla superficie
matematica di riferimento. Si produce un rapporto testuale che mostra i valori
dell’ispezione.
-Geomagic
Studio1.0- stima: le curvature, le isofote, e le deviazione
standard
fra modello numerico e matematico, con scala di colore e rapporti testuali.
-RealWorks-
le
possibili deviazioni sono stimate con curve sulla
nuvola di punti.
-MATCHGRAPH-
Compara superfici Nurbs e nuvola di punti graficizzando i modelli in
scala di colore.
[2] NURBS: acronimo di Non Uniform Rational B-Spline. Identifica curve e superfici spline con distribuzione dei punti di controllo e peso degli attrattori variabili.
[3] TOF: Acronimo di Time of Flight, individua la tecnica di scansione laser detta A Tempo di Volo.
[4] Tratto da N. Alberto Borghese, Costruzione di Modelli 3D del Volto e loro Animazione, in www.inb.mi.cnr.it/Borghese/Borghese.html.
[5] Michael Garland e Paul Heckbert. Surface simplification using quadric error metrics. Proceedings of SIGGRAPH 97, 1997.
[6] curva che nasce negli anni 50’ all’interno dell’industria automobilistica Renault per opera del matematico P. Bézier. La curva di Bézier è descritta matematicamente da un polinomio; graficamente è definita da punti di appoggio, o punti di interpolazione, e da tangenti alla curva stessa.
[7] Patch: superfici molto utilizzate nella modellazione organica dato il livello di accuratezza con il quale tracciano superfici curve. Queste superfici, di Coons, sono generate dall’interpolazione di quattro curve contigue. Quando le quattro curve sono bordi di altre superfici viene mantenuta la continuità di tangenza e curvatura.
- A.A.V.V., Frontiere del Rilievo. Dalla matita alle scansioni 3D, Strumenti del Dottorato di Ricerca, a cura di Riccardo Migliari, Gangemi, Roma2001.
- Wolfgang BOEHLER, Guido Heinz, Andreas Marbs, Mirko Siebold, 3D Scanning Software: An Intoduction, i3mainz, Institute for Spatial Information and Surveying Technology, FH Mainz, University of Applied Sciences,Holzstrasse 36, 55116 Mainz, Germany.
- N. Alberto Borghese, Costruzione di Modelli 3D del Volto e loro Animazione, in www.inb.mi.cnr.it/Borghese/Borghese.html.
- Edmond Boyer, Sylvain Petitjean, Curve and Surface Reconstruction From Regular and Non-Regular Point Sets.
- Nicola Brusco, Metodi volumetrici per la costruzione di superfici tridimensionali, Tesi di Laurea, Relatore: prof. G. M. Cortellazzo, Università di Padova, Dip. di Elettronica ed Informatica, Padova 2002.
- Massimiliano Ciammaichella, Superfici. La pelle dell’ @rchitettura contemporanea, Tesi di Dottorato di Ricerca in Rilievo e Rappresentazione dell’Architettura e dell’Ambiente, Tutor: prof. Riccardo Migliari, Facoltà di Architettura di Roma "La Sapienza", Roma 2002.
- S. Karbacher, Discrete Modeling of Point Clouds.
- Riccardo Migliari, Geometria dei modelli, Kappa, Roma 2003.
- Riccardo Migliari, Disegno come Modello, Kappa, Roma 2004.
- Les Piegl, Wayne Tiller, The NURBS Book, Springer, Berlino 1997.
- Mark Soucy, Denis Laurendeau, A General Surface Approach to the Integration of a Set of Range Views, IEEE Transaction on Pattern Analysis Machine Intelligence, vol. 17, no. 4, april 1995.