Sullo schema geometrico costruttivo degli anfiteatri romani:
gli esempi del Colosseo e dell'Arena di Verona

Camillo Trevisan
trevisan@iuav.it

Articolo pubblicato sul numero 18/19 (Giugno 2000) della rivista Disegnare idee e immagini 

Per accedere a questa stessa pagina con immagini in formato DWF
Nota sulla visualizzazione delle immagini DWF: le immagini sono di tipo vettoriale (consentendo, dunque, l'ingrandimento interattivo di porzioni specifiche, l'attivazione e la disattivazione di layer, ecc.). E' dunque necessario disporre di un apposito plug-in, ad esempio Whip! presso il sito: http://www3.autodesk.com/adsk/section/0,,163301,00.html

Per accedere alla pagina contenente il software di interpolazione di punti mediante ellissi, ovali a 4 centri e ovali a 8 centri

Per accedere alla pagina contenente le misure degli anfiteatri (da Jean-Claude Golvin, L'Amphithéâtre romain: essai sur la théorisation de sa forme et de ses fonctions, Boccard, Paris 1988)

Per copiare i file contenenti i punti di controllo rilevati nell'Arena di Verona.

Nel suo fondamentale studio sugli anfiteatri, Mark Wilson Jones propone che l'architetto romano iniziasse la fase di progetto di un anfiteatro con uno schema provvisorio - basato sul triangolo rettangolo perfetto con proporzioni tra i lati 3:4:5 o sul semi triangolo equilatero -, ampliandolo o riducendolo per far sì che gli archi perimetrali raggiungessero la larghezza voluta.[1]

Questo studio, sulla scorta di accurati rilievi topografici del Colosseo[2] e dell'Arena di Verona[3] e di considerazioni sulla geometria e sulla forma delle ellissi e degli ovali, propone una semplificazione ed una generalizzazione del dispositivo progettuale indicato da Wilson Jones e da varie altre fonti.[4]

Una prima osservazione riguarda le caratteristiche geometriche delle sezioni orizzontali dei due anfiteatri rilevati. Interpolando insiemi di punti riferiti con certezza a strutture originali emerge con chiarezza una notevole analogia tra i due esempi: in entrambi i casi gli ovali a quattro centri interpolano solo a grandi linee le strutture perimetrali, con scarti quadratici medi superiori ai 15 centimetri. Ma è soprattutto la disposizione e la conformazione degli scarti a rendere quasi impossibile ritenere costruttive quelle curve: i punti rilevati, infatti, si dispongono, per sottoinsiemi e con simmetrica regolarità, alternativamente all'interno o all'esterno della curva interpolante (vedi figura 1).

Figura 1
Confronto tra i punti topografici rilevati e gli ovali a 4 centri che meglio li interpolano (particolare del Colosseo).

Viceversa, sia ovali a otto centri sia ellissi, non solo interpolano i punti con scarti più che dimezzati, ma anche con distribuzione degli errori più indifferenziata e casuale. D'altra parte, uno scarto di alcuni centimetri è facilmente giustificabile, tenendo conto delle inevitabili imprecisioni costruttive e, soprattutto, dell'azione anisotropa degli agenti atmosferici e dei secoli, oltre alla subsidenza del suolo. Purtroppo, la grande affinità di forma tra le due curve, pur geometricamente così diverse tra loro, e gli scarti simili rendono impossibile stabilire per questa via la vera forma di quegli anfiteatri: il risultato della prima fase di studio, se tende ad escludere l'ovale a quattro centri, rende però plausibili sia l'ellisse sia l'ovale a otto centri. Questo comporta un problema di difficile soluzione: se si esclude l'ovale a quattro centri, come calcolare con sufficiente esattezza il perimetro e l’area della curva? Identificare il perimetro di un’ellisse o il perimetro e l’area di un ovale a otto centri comporta, infatti, calcoli assai più complessi rispetto all'ovale più semplice; ma d’altra parte è necessario conoscere quei dati per progettare la capienza della cavea e il numero e l’interasse degli archi esterni.

È perciò interessante tentare di delineare un metodo non solo semplice, completo e verificabile, ma anche univoco, adottabile integralmente in molti altri anfiteatri simili, stabilendo la loro forma a partire dai dati di rilievo e riducendo al minimo le ipotesi, le modifiche e le varianti.

Il procedimento qui proposto possiede buona parte di queste caratteristiche, anche se gli esempi studiati, pur rappresentativi, sono tuttavia ancora troppo pochi per poter sostenere la sua validità assoluta.

Schematizzando, dopo aver identificato e rilevato topograficamente uno o più insiemi di punti che definiscono, possibilmente in modo completo, curve appartenenti ad elementi architettonici certamente non manomessi, si operano i passi che seguono.

A) Gli insiemi di punti sono interpolati, separatamente uno dall'altro, con ellissi, ovali a 4 e a 8 centri (vedi appendice A).

Le interpolazioni saranno ripetute più volte, usando sottoinsiemi di punti scelti casualmente e riguardanti il 50% e il 75% degli insiemi completi. Questo primo passo fornisce alcune prime importanti indicazioni:

- Anzitutto, sull'omogeneità intrinseca dei singoli insiemi di punti nel caso, ad esempio, le interpolazioni di sottoinsiemi diversi di punti appartenenti alla stessa curva producano dati simili oppure difformi tra loro per quanto concerne gli scarti quadratici medi, le lunghezze degli assi, le loro rotazioni o la posizione dei centri delle curve interpolate. In altre parole, rispondendo alla domanda: rilevando altri punti, appartenenti alla stessa curva, i risultati si modificano? E in che modo?

- Sul confronto tra diversi insiemi di punti e, dunque, tra curve in teoria concentriche ed equidistanti. I vari centri dovrebbero essere molto vicini tra loro, così come le varie rotazioni degli assi; la differenza tra i semiassi dovrebbe essere quasi costante. Inoltre, gli scarti dovrebbero essere coerenti tra loro per ciascun tipo di curva, salvo il caso in cui i vari insiemi di punti si riferiscano ad elementi architettonici disomogenei tra loro per degrado o dissesto statico.

- Sul valore assoluto e relativo degli scarti e sulla loro struttura. Ancor più importante del valore assoluto, è infatti interessante analizzare la distribuzione e la caratterizzazione degli errori; se questi si distribuiscono in modo isotropo e casuale oppure si concentrano in aree specifiche: in tal senso la doppia simmetria tipica degli anfiteatri è molto utile per un confronto sulle modulazioni e le ripartizioni degli scarti.

- Le migliori interpolazioni della curva più esterna e della più interna, se disponibili, forniscono dati attendibili sulle lunghezze degli assi dell'anfiteatro e dell'arena e, più in generale, sulla differenza di lunghezza tra gli assi, un dato assai notevole ed indicativo, come si vedrà in seguito.

B) Gli insiemi di punti sono interpolati, tutti assieme, con ovali a 4 e a 8 centri mantenendo unici per tutti il centro delle curve, i triangoli generatori e la rotazione degli assi. Sono anche interpolati con ellissi, mantenendo costanti il centro, la rotazione degli assi e l'equidistanza tra le curve sugli assi (vedi appendice A) e facendo variare liberamente i fuochi.

Questo passaggio consente un ulteriore controllo, incrociando i risultati con quelli ottenuti nel passo precedente. È qui interessante osservare e valutare come e di quanto variano gli scarti, le lunghezze degli assi e le loro differenze, le posizioni dei centri e le rotazioni degli assi.

Probabilmente si potranno ora formulare alcune ipotesi sulla forma dell'anfiteatro oppure, almeno, escluderne alcune altre. Di norma le differenze tra ellissi ed ovali a 8 centri sono minime, mentre appaiono più marcate le difformità tra queste due curve e l'ovale a 4 centri e pertanto sarà possibile assegnare diversi gradi di attendibilità ai vari tipi di curve (vedi appendice B).

C) Reperimento del più probabile coefficiente di trasformazione metro/piede romano (o altra eventuale unità di misura). D'ora in poi, infatti, tutte le analisi e le valutazioni dovranno essere compiute in piedi romani e non più in metri. Poiché non vi è la certezza assoluta sulla lunghezza del piede romano usato per quell'anfiteatro, si dovrà operare all'interno di un ambito di diverse possibilità, ad esempio, con un valore compreso tra 29.3 e 29.8 centimetri.[5]

Questo passo è particolarmente delicato poiché introduce un fattore di scala assolutamente non valutabile con certezza (se, ad esempio, la lunghezza da trasformare è 90 metri, l’equivalente misura in piedi può variare, nelle ipotesi fatte, tra 302 e 307). Per ridurre le possibilità di errori, il dato forse più interessante è costituito dalla differenza tra le lunghezze dei due semiassi, legata strettamente alle dimensioni dell'arena ed ai triangoli generatori. Questo valore, di norma piccolo ma costante, consente una migliore approssimazione all’intero più vicino. In ogni caso sarà utile, per ciascuna ipotesi prodotta, verificare nuovamente i limiti inferiori e superiori delle lunghezze dei parametri essenziali.

D) Esame delle convergenze dei setti radiali. In alcuni casi (ad esempio, nell’anfiteatro di Pozzuoli) i setti convergono approssimativamente verso il centro, in molti altri (ad esempio nel Colosseo, nell’Arena di Verona, a Capua e Thysdrus) verso due punti che spesso sono anche i vertici del triangolo generatore. Poiché una piccola imprecisione nella costruzione o nel rilievo di un setto radiale è notevolmente amplificata nel prolungamento del segmento, questa fase di analisi potrà essere ripetuta al contrario: dopo aver identificato i probabili punti di convergenza (i possibili vertici del triangolo generatore) si potrà verificare lo sbandamento dei setti rispetto alle semirette lanciate da quei punti.

Le maggiori incertezze probabilmente si noteranno nei setti di passaggio, quelli posti nelle vicinanze di un raccordo tra i vari archi di cerchio o in ogni modo nei setti più lontani dagli assi.

E) Giunti a questo punto dello studio, si è già in possesso di una gran mole di informazioni e si potranno senz’altro assegnare pesi e gradi di probabilità alle varie congetture sulla forma e le dimensioni dell’anfiteatro.

Nei due casi esaminati in dettaglio (vedi appendici C e D) si riscontrano alcune analogie:

- Il rapporto tra gli assi dell’arena è vicino a 5/3.

- Le varie curve sono meglio interpolate con ovali a 8 centri o ellissi[6] rispetto agli ovali a 4 centri.

- Nell’interpolazione con ovali a 8 centri, il rapporto tra le distanze dal centro dell’ovale dei due centri di curvatura posti sugli assi è vicino a 5/6, pur con alcune possibili variazioni (vedi appendice A).

- Il centro di curvatura posto sull’asse minore non varia molto nelle interpolazioni con ovali a 4 e a 8 centri (considerando anche l’instabilità intrinseca di quelle curve, soprattutto l’ultima).

- La distanza tra questo centro di curvatura e il centro dell’ovale è circa pari alla differenza tra gli assi.

- I due centri di convergenza dei setti radiali sono compatibili con le posizioni dei centri di curvatura dell’ovale a 4 centri.

Si è così formulata un’ipotesi che prevede due fasi distinte: la prima, che potremmo definire progettuale, impiega l’ovale a 4 centri; la seconda, esecutiva, si serve dell’ovale a 8 centri oppure anche, in teoria, dell’ellisse.

Il progetto di un anfiteatro, infatti, deve coordinare tra loro le dimensioni dell’arena, quelle della cavea e la lunghezza del perimetro esterno, per il calcolo delle larghezze degli archi, oltre all’area. Tutti questi elementi devono essere facilmente determinabili e concorrere all’identificazione di una curva da tracciare con semplicità.

La prima fase, di calcolo e di progetto, prevede dunque la definizione del rapporto tra gli assi dell'arena, delle loro dimensioni e del numero e del passo degli archi esterni.

Permette di calcolare facilmente le lunghezze degli assi e il perimetro esterno della cavea, i perimetri interni (e dunque il passo degli archi più interni) e le aree.

Se il rapporto scelto tra gli assi dell’arena è di 5/3 (come nei casi studiati), il triangolo generatore avrà rapporti tra i lati 3:4:5 e le lunghezze dei lati saranno moltiplicate per un modulo di scala che corrisponde alla metà della differenza tra i semiassi dell’arena. Questi, infatti, avranno lunghezze pari al cateto minore e all’ipotenusa del triangolo perfetto 3:4:5.

Per il progetto della cavea e per il calcolo del perimetro esterno dell’anfiteatro ci si servirà sia del valore 22/7 per p, sia di un’ottima approssimazione degli angoli acuti del triangolo 3:4:5, rispettivamente pari a 13/22 e 9/22 di un angolo retto (vedi appendice B.1). Queste approssimazioni introducono, rispetto alla vera misura, un errore complessivo dello 0.014%.

Poiché, fissati gli assi, la lunghezza del perimetro di un ovale a 4 centri non si discosta da quella di un’ellisse o di un ovale a 8 centri (vedi appendice B.4), i calcoli eseguiti rimangono validi anche se la curva finale è ‘addolcita’, specie in vicinanza dei punti di raccordo, usando operativamente un ovale a 8 centri o un’ellisse.

Nel caso dell’ovale a 8 centri – forse più probabile, non fosse altro che per la conservazione del tipo di curva –, questo è definito assai semplicemente tenendo immobile un vertice del triangolo usato per il calcolo dell’ovale a 4 centri (quello posto sull’asse minore), traslando l’altro di un terzo del modulo di scala e fissando il terzo polo per trilaterazione (vedi appendice B).

Il cambio di curva, tra la fase progettuale e quella esecutiva, giustifica i dati dei rilievi – contrastanti con l’ovale a 4 centri – ma contemporaneamente consente l’uso di quest’ultima curva, più semplice, per tutti i calcoli ed i controlli progettuali.

Al riguardo è utile osservare che i dati ottenuti nella fase di compensazione e relativi ai triangoli generatori degli ovali, soprattutto per gli ovali a 8 centri, non sono però decisivi e definitivi, poiché gli scarti variano di poco modificando leggermente le proporzioni dei triangoli generatori. È pertanto interessante, per queste curve, interpolare nuovamente i dati imponendo non tanto misure ma proporzioni prestabilite tra i lati dei triangoli generatori, verificando poi l'andamento degli scarti quadratici medi sui punti di controllo e i valori assoluti delle lunghezze dei lati e, soprattutto, degli assi (vedi, ad esempio, la tabella D.1).

F) Un’ultima verifica, pur non strettamente e direttamente legata alla ricerca della forma, consiste nell’indagare sulle proporzioni e i rapporti tra gli elementi geometrici di progetto e l’architettura costruita.

Un’eventuale conferma in tal senso – come, ad esempio, sembra emergere dai dati del Colosseo – rafforzerebbe notevolmente le ipotesi proposte e consegnerebbe loro una forte valenza compositiva, oltre che progettuale e funzionale.

In conclusione, la procedura qui proposta prende spunto da autorevoli studi precedenti ed individua – sulla scorta di indispensabili rilievi topografici – due distinte fasi di elaborazione, separando il calcolo e il progetto (ovale a 4 centri, con la proposta di una semplificazione del calcolo del perimetro) dall’esecuzione (ellisse o, più verosimilmente, ovale a 8 centri).

Le due fasi sono in tal modo coordinate tra loro – slegando, inoltre, la scelta delle dimensioni dell’arena da quelle della cavea, come è illustrato nella figura 2 – e sono pienamente compatibili con gli esempi studiati e, forse, anche con altri anfiteatri simili a questi.

Figura 2
Confronto dei cinque anfiteatri studiati, mantenendo costanti le dimensioni dell’arena (tutte con la stessa proporzione tra gli assi). Individuazione del terzo centro di un ovale a 8 archi. Il punto D si trova su di una ellisse che ha per fuochi i punti A’ e B e come somma delle distanze dai fuochi la differenza tra BH e A’L. In blu gli ovali a 4 centri, in rosso l’ovale a 8 centri, per un confronto.    

Appendice A.  Software per l'interpolazione di ellissi ed ovali a 4 e 8 centri[7]

Per eseguire delle valutazioni approfondite sulla genesi geometrica delle curve costruttive di un anfiteatro si sono messi a punto degli specifici programmi per computer. I programmi interpolano un insieme di punti di controllo, calcolando i parametri relativi ad un’ellisse oppure ad un ovale definito da 4 oppure 8 centri generatori, in modo da rendere minimo lo scarto quadratico medio delle distanze dei punti dati dalla curva interpolante trovata.

I programmi richiedono l'inserimento dei valori iniziali approssimati dei parametri che definiscono le curve (comprese la traslazione del centro e la rotazione degli assi), fornendo, dopo alcune iterazioni, i coefficienti finali e tutti gli scarti (le distanze tra ciascun punto di controllo e la curva interpolante trovata), oltre alle curve stesse, nel formato grafico DXF.

Nei due programmi per l'interpolazione di ovali il numero degli insiemi di punti di ingresso può essere compreso tra 1 e 30, ciascuno con un massimo di 2000 punti: in questi casi gli ovali concentrici mantengono invariati alcuni parametri (i cateti dei triangoli generatori, oltre alle coordinate X, Y del centro e la rotazione degli assi di simmetria) e pertanto possono essere interpolate contemporaneamente più curve concentriche ed equidistanti. Nel programma Ellisse è prevista, di norma, una sola curva di ingresso: infatti, ellissi concentriche, coassiali ed equidistanti sugli assi di simmetria sono caratterizzate da fuochi diversi. Nel caso siano presenti più curve, sarà mantenuta costante la distanza tra i fuochi e, pertanto, le varie ellissi interpolanti non saranno parallele tra loro, pur mantenendo lo stesso centro e la stessa rotazione degli assi.

Il metodo di calcolo consiste nel trovare – per mezzo di algoritmi pseudostocastici e operando per ‘saturazione’ – la sella minima di un’ideale superficie, definita dagli infiniti scarti quadratici medi ottenuti variando i parametri generatori: nel caso i valori iniziali siano vicini a quelli finali tale ricerca sarà condotta senz'altro con successo; viceversa, potrebbe accadere che l'algoritmo iterativo venga ‘catturato’ da un minimo locale, posto sul ‘percorso’ di calcolo tra il punto di partenza, definito dai valori iniziali, e il vero minimo assoluto. In tutti i casi è utile verificare il buon esito dell'iterazione, modificando i valori di partenza e controllando che, al contrario, i valori finali rimangano costanti.

Da notare, infine, che i due programmi per l'interpolazione di ovali sono necessariamente tendenzialmente instabili: infatti, mentre nel caso dell'ellisse il programma deve verificare la coerenza dei dati rispetto ad un'unica curva, per l'ovale la verifica deve essere eseguita su quattro o otto archi di cerchio. Mentre, fissati i due semiassi, esiste una sola ellisse con quei valori, al contrario esistono infiniti ovali - sia a 4 sia a 8 centri - con le stesse misure degli assi e diversa curvatura: nel caso degli ovali, pertanto, diviene indispensabile disporre di punti di controllo posti nelle vicinanze dei raccordi tra gli archi.

Per l’analisi compiuta sul Colosseo e l’Arena di Verona sono stati approntati anche programmi specifici, non disponibili in Internet, utili, ad esempio, all’interpolazione di più ellissi variando liberamente e indipendentemente i fuochi di ciascuna ma tenendo costante la distanza tra le curve sugli assi[8] e, soprattutto, la rotazione degli assi ed il loro centro. Oppure, programmi per l’interpolazione con ovali imponendo però il rapporto tra i lati dei triangoli generatori: in tal modo è stata identificata la scala finale dei triangoli e degli assi, confrontandola con le ipotesi di partenza.

Appendice B.  Confronto tra l'ellisse e gli ovali a 4 e 8 centri

In questa breve appendice sono presentate alcune considerazioni, note e analisi, utili per la completa descrizione del tema. Molte di queste sono già state ampiamente studiate e commentate[9], tuttavia è conveniente raccoglierle e illustrarle complessivamente, trascurando le più elementari.

B.1. Ovali a 4 centri
Dati gli assi, si possono costruire infiniti ovali a 4 centri, modificando opportunamente il triangolo rettangolo generatore.
Definiti i semiassi (S1 il maggiore, S2 il minore), si può sempre trovare un triangolo che costruisce l'ovale mediante la formula: S = (S1-S2)/(A+B-C) (1), dove A e B sono i cateti del triangolo (con A di norma posto sul semiasse maggiore e B sul minore), C l'ipotenusa ed S è il coefficiente di scala del triangolo scelto. Così, se S1 è pari a 135 ed S2 a 81, il triangolo rettangolo 3:4:5 fornisce un fattore di scala di 27 (triangolo generatore 81 : 108 : 135). Ma anche, ad esempio, il triangolo 1:1.5:1.8027756 genera un proprio fattore di scala: in questo caso sarà un numero irrazionale, pari a 77.44996 (triangolo generatore 77.44996 : 116.1749 : 139.6249).

Infatti, definiti R1 il raggio minore ed R2 il raggio maggiore dell'ovale, sussistono senz'altro le relazioni:

A+R1=S1 (2), (cateto minore del triangolo generatore + raggio minore = semiasse maggiore);

R2-B=S2 (3), (raggio maggiore - cateto maggiore del triangolo generatore = semiasse minore);

R1+C=R2 (4), (raggio minore + ipotenusa del triangolo generatore = raggio maggiore).

Dunque, se infiniti triangoli rettangoli possono definire un dato ovale a 4 centri[10] - a meno di un fattore di scala -, tuttavia esistono due triangoli dalle caratteristiche assai peculiari, e non solo per questa specifica particolarità: il triangolo 3:4:5 è il solo triangolo, con cateti interi, che genera un ovale avente semiassi interi e delle stesse lunghezze di un cateto e dell'ipotenusa (rapporto 5/3); mentre il triangolo avente un cateto pari all'unità, l'ipotenusa di lunghezza 2 e il cateto maggiore pari alla radice quadrata di 3 (metà del triangolo equilatero) è l'unico triangolo notevole a definire un ovale con i semiassi aventi lunghezze pari ai due cateti del triangolo (rapporto di radice di 3). Questi due triangoli sono i soli, con almeno due lati interi, a trasmettere direttamente le misure di due lati a quelle dei due semiassi dell'ovale.

Naturalmente esistono molti altri triangoli con caratteristiche vicine a quelle del triangolo semi equilatero, vale a dire con rapporti tra i cateti molto vicini alla radice quadrata di 3: ad esempio, il triangolo 4:7:8 (in realtà 8.0623), oppure 11:19:22 (21.9545) o anche 15:26:30 (30.0167).[11]

Per quanto concerne il calcolo della lunghezza complessiva della curva, questo evidentemente prevede la conoscenza dell'esatto valore di p e degli angoli compresi tra i cateti e l'ipotenusa del triangolo rettangolo (questi ultimi di assai semplice identificazione per il triangolo semi equilatero). Wilson Jones[12] propone l'uso di 22/7 come eccellente approssimazione di p (scarto 0.04%) e formula anche un'ipotesi per un calcolo semplificato della lunghezza: P = (L + H) * p / 2, dove P è la lunghezza della curva, L l'asse maggiore, H l'asse minore dell'ovale. Questa formula approssima la vera lunghezza con scarti compresi tra lo 0.5 e l'1.25%, in funzione del rapporto tra gli assi.

Tuttavia, è senz'altro più corretto applicare la vera formula di calcolo – usando le proporzioni tra angoli e archi sottesi -, nella quale, oltre all'uso del p, l'unica difficoltà è data dalla necessità di conoscere gli angoli acuti del triangolo rettangolo generatore. Infatti, limitando il calcolo ad un quadrante dell'ovale, la lunghezza del quarto di perimetro è data dalla somma di due archi di circonferenze diverse tra loro. In termini moderni:

P4 = (2 * p * R1 * X1) + (2 * p * R2 * X2) (5), dove P4 è un quarto della lunghezza, R1 ed R2 il raggio minore e maggiore e X1 e X2 le due frazioni, rispetto a 360°, degli angoli acuti del triangolo rettangolo generatore (con X1+X2 = 90°/360°).

Se il calcolo si riferisce al triangolo semi equilatero gli angoli sono immediatamente individuabili e la (5), compiendo un errore dello 0.04% dovuto solo alla stima di p, si semplifica in: P4 = (22/21 * R1) + (11/21 * R2) (6)

Ed è inoltre da considerare che, in ogni caso, i due raggi sono legati tra loro, poiché il raggio maggiore è pari al raggio minore sommato all'ipotenusa del triangolo.

Un po' meno precisa, in teoria, è la stima della lunghezza nel caso del triangolo 3:4:5, poiché in questo caso gli angoli non sono esprimibili come numeri razionali. Ma le caratteristiche di quel triangolo erano certamente assai note in quel tempo e non è impossibile ipotizzare che siano state compiute approfondite osservazioni anche sui suoi angoli acuti. In realtà questi due angoli sono identificabili, con ottima approssimazione, come frazioni di interi piccoli, 13/22 e 9/22 di un angolo retto, introducendo un errore relativo dello 0.097%.

Il calcolo della lunghezza di un quarto del perimetro, dato il ripetersi del numero 22, si semplifica in:

P4 = (13/14 * R1) + ( 9/14 * R2) (7), la quale – poiché R2 = R1 + C, dove C è l’ipotenusa del triangolo rettangolo generatore – equivale all’equazione: P4 = (11/7 * R1) + (9/14 * C) (8)

Da quest’ultima segue: R1 = (7/11 * P4) – (9/22 * C) (9)

In questo caso l’errore complessivo, compresa la stima di p e per rapporti tra gli assi simili a quelli in esame, si assesta attorno allo 0.014%. Un errore anche minore del precedente, dunque, poiché la suddivisione frazionaria degli angoli compensa parzialmente la stima del valore di p.

B.2. Ovali a 8 centri

Anche in un ovale a 8 centri, definiti gli assi, esistono infinite possibili varianti, sia per quanto riguarda i triangoli generatori, sia per le lunghezze dei raggi. Non solo, infatti, sussistono infinite combinazioni per il raggio minore (R1) e quello maggiore (R3), come nell'ovale a 4 centri; ma anche altrettante infinite possibilità di scelta per il raggio intermedio (R2). L'unica restrizione è data dalla necessità che il centro dell'arco intermedio giaccia su di una ellisse che ha i primi due centri (di R1 ed R3) come fuochi e la differenza tra i due raggi (R3-R1) come somma delle distanze dai fuochi (vedi figura 2). Infatti, definita come D1 la distanza tra il centro di R1 e il centro di R2 e D2 la distanza tra i centri di R3 ed R2, sussiste l'uguaglianza:

R1+D1 = R2 = R3-D2 (10), dalla quale segue: D1+D2 = costante = R3-R1 (11).

Nota questa relazione, dunque, è estremamente semplice definire e tracciare l'ovale a 8 centri, poiché, per trovare il terzo centro, è sufficiente eseguire una sola, semplice, trilaterazione. La curva così ottenuta - per rapporti tra gli assi vicini a quelli delle curve esterne degli anfiteatri - è molto simile all'ellisse e una variazione, anche notevole, della posizione del centro dell'arco intermedio non modifica sostanzialmente la lunghezza della curva (vedi paragrafo B.4).

B.3. Ellissi

In questo caso, date le lunghezze dei due assi, questi definiscono una ed una sola ellisse. L'asse maggiore è anche pari alla somma delle distanze di ciascun punto dell'ellisse dai due fuochi e, pertanto, puntando il compasso su di un estremo dell'asse minore, con apertura pari al semiasse maggiore, l'arco di cerchio così tracciato taglia l’asse maggiore nei due fuochi. Queste caratteristiche, come è noto, rendono l'ellisse semplice da individuare e tracciare, quasi quanto l'ovale.

Assai più complesso è invece il calcolo della lunghezza della curva. Ed è questo il motivo principale che porta ad escludere l'ellisse come prima ed unica curva di progetto: infatti, in tal modo, risulta difficile trovare il fattore di scala necessario per il calcolo delle lunghezze degli interassi degli archi perimetrali.

È infine interessante notare che, pur non esistendo ellissi concentriche parallele[13], è tuttavia possibile costruire curve parallele ad un’ellisse: sia dall’arena verso l’esterno della cavea, sia viceversa. Mentre la differenza tra un’ellisse e il corrispondente ovale a 8 centri aumenta con l’aumentare del rapporto tra gli assi – passando, ad esempio, dalla quasi coincidenza all’esterno ad una reale differenza sull’arena –, la curva costruita parallelamente all’ellisse mantiene costanti le differenze percentuali dal corrispondente ovale a 8 centri (vedi figura 3). Tuttavia, la compensazione separata delle singole curve del Colosseo non ha mostrato sostanziali difformità dal calcolo compiuto su tutte le curve compensate assieme (vedi tabella C.1).

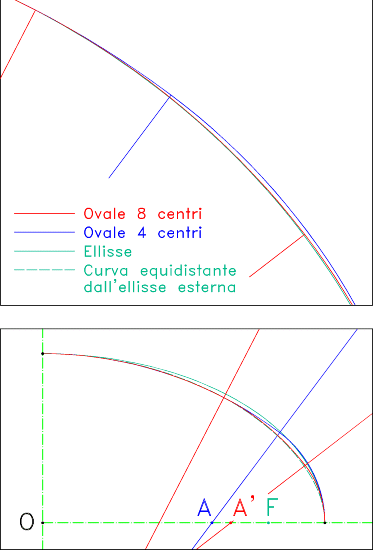
Figura 3
Confronto tra curve caratterizzate da un diverso rapporto tra gli assi. In basso l’arena, in alto una porzione del perimetro esterno. Da notare l’aumento della distanza tra l’ovale a 8 centri e l’ellisse con l’aumentare del rapporto tra gli assi. Al contrario, la curva parallela all’ellisse esterna descrive l’arena in quasi completa coincidenza con l’ovale a 8 centri.

B.4. Confronto tra le lunghezze delle curve

Infine, è interessante approfondire un altro importante quesito: stabiliti gli assi – oppure anche i raggi, per gli ovali –, di quanto si discostano tra loro le lunghezze dell'ellisse e dei vari possibili ovali a 4 e a 8 centri?

La risposta a questo quesito potrebbe risultare esiziale per l'ipotesi fatta, poiché quest’ultima si fonda proprio sulla sostanziale equivalenza tra le lunghezze delle varie curve, pur nella loro grande differenza geometrica e costruttiva.

Stabilito un esempio simile all'ipotesi fatta per il Colosseo (semiassi 318 e 264 piedi), la lunghezza dell'ellisse è 1832.34 piedi, quella dell'ovale a 4 centri (triangolo generatore 81:108:135) è 1836.61 piedi (1836.86 se calcolato per mezzo della (7)), mentre quella dell'ovale a 8 centri (90:108 e con 144 piedi di differenza tra il raggio maggiore e il minore) è 1832.74 piedi.

La differenza tra ovali a 4 e a 8 centri è dunque di circa 0.05 piedi per ciascun arco, circa un centimetro e mezzo. Dunque, nella pratica operativa non si sarebbe rilevato alcun errore, pur costruendo due curve assai diverse tra loro.

Appendice C.  Il Colosseo

Il rilievo topografico ha permesso di identificare sette insiemi di punti che si riferiscono a curve complete o parziali.

La compensazione di sottoinsiemi di punti ha portato a modeste variazioni delle lunghezze degli assi e degli scarti quadratici medi, contenute le prime in ± 5/6 centimetri, secondo il tipo di curva, gli ultimi in ± 0.4 cm (si veda la figura 4).

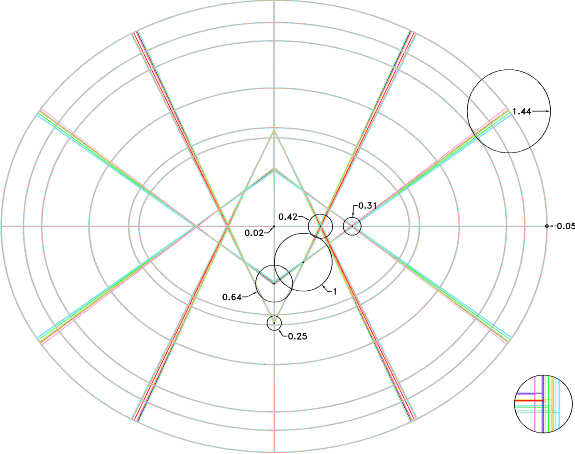
Figura 4
Interpolazioni contemporanea con ovali a 8 centri, usando sottoinsiemi scelti casualmente del 50% e 75% dell’insieme complessivo dei punti di controllo. I cerchi, ingranditi di 10 volte, indicano l’ambito di errore espresso in metri. In basso a destra, l’ingrandimento di 100 volte dell’estremità destra degli assi maggiori degli ovali.

Le interpolazioni possono dunque considerarsi stabili, anche perché, variando i parametri iniziali del 15/20%, i risultati convergono regolarmente allo stesso minimo (differenze di SQM inferiori al millimetro), ad esclusione dei valori relativi ai lati dei triangoli – per gli ovali a 8 centri – che possono variare anche sensibilmente a parità di scarto finale. In particolare, la variazione si accentua con il mutare degli accoppiamenti tra gli insiemi di punti: ad esempio compensando assieme le curve 3 e 5, oppure le 3, 4, 5 o le 3, 5, 6. Del resto, questa circostanza era ampiamente prevista, per le stesse caratteristiche geometriche di quelle curve: per gli ovali a 8 centri sarà dunque quasi impossibile stabilire i parametri definitivi per questa via.

Nell’ovale a 4 centri, le curve interpolate separatamente definiscono tuttavia dei triangoli generatori molto simili tra loro (ad esclusione della curva più interna, ma solo per quanto riguarda il punto sul semiasse minore, con distanza di circa 4 metri), con differenze tra i vertici dei triangoli anche di ± 60/70 cm, ma rapporto tra i cateti sempre vicino a 4/5 (vedi figura 5).

Figura 5
Colosseo. Interpolazione separata dei vari insiemi di punti con ovali a 4 centri.

Il confronto tra i risultati ottenuti dalla compensazione separata o complessiva dei vari insiemi di punti conferma il grado di affidabilità dei risultati, poiché non si riscontrano differenze di rilievo, a parità di curve, sia nelle traslazioni dei centri o nelle rotazioni degli assi, sia negli SQM (vedi tabelle C.1 e C.2 e figure 6..10, relative alle diverse curve compensate assieme o una per volta). I dati relativi alle lunghezze degli assi mostrano variazioni assolute anche di 20/30 centimetri, da curva a curva, e variazioni di norma molto più contenute tra le stesse curve compensate assieme alle altre o separatamente.

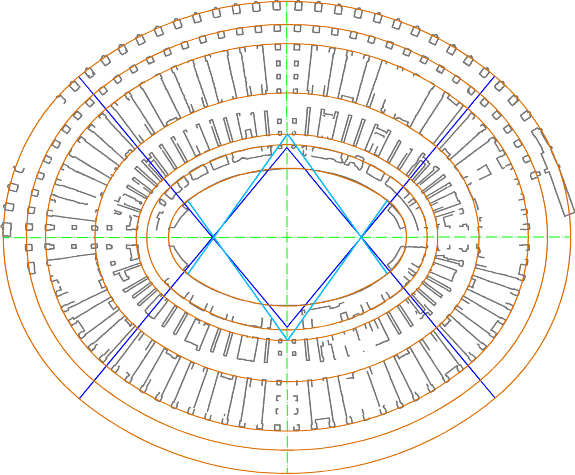
Figura 6
Colosseo. Interpolazione contemporanea (ad esclusione della curva più interna) dei vari insiemi di punti con ovali a 4 centri.

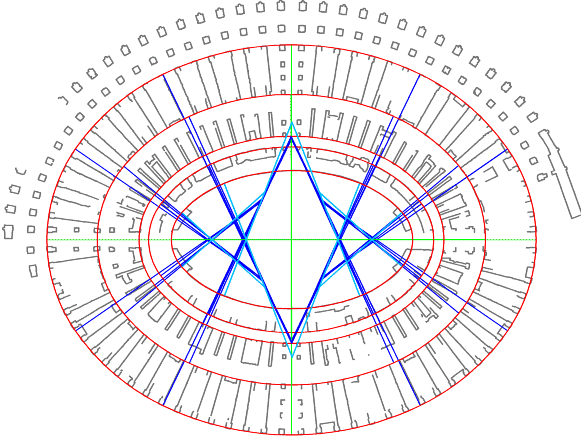
Figura 7
Colosseo. Interpolazione separata dei vari insiemi di punti con ovali a 8 centri.

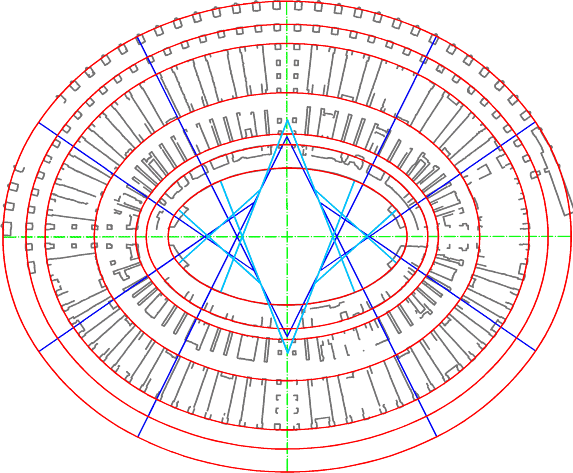
Figura 8
Colosseo. Interpolazione contemporanea (ad esclusione della curva più interna) dei vari insiemi di punti con ovali a 8 centri.

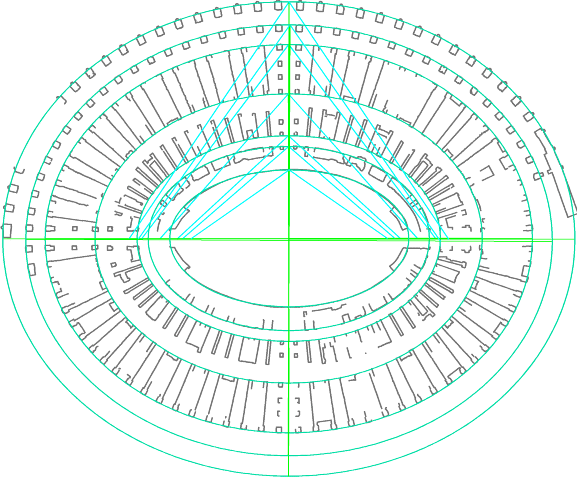
Figura 9
Colosseo. Interpolazione separata dei vari insiemi di punti con ellissi.

Figura 10
Colosseo. Interpolazione contemporanea (ad esclusione della curva più interna) dei vari insiemi di punti con ellissi.

Sintetizzando, una prima importante conclusione porta a considerare molto attendibili i valori ottenuti per le lunghezze e le rotazioni degli assi e le traslazioni dei centri (in quest’ultimo caso con scarti leggermente superiori alla norma nelle ellissi), meno certi quelli relativi alle lunghezze dei lati dei triangoli generatori, soprattutto per gli ovali a 8 centri.[14]

Un’altra interessante osservazione riguarda la curva più interna: essa sembra seguire altre logiche rispetto a quelle esterne, molto più omogenee tra loro. Compensata da sola produce degli scarti in linea con le previsioni, ma con parametri relativi ai triangoli generatori – o all’equidistanza dalla penultima curva, nel caso dell’ellisse – molto diversi dalle altre. Compensata assieme alle altre aumenta di molto lo scarto complessivo. Infatti, è molto più schiacciata sull’asse minore, ridotto di circa 4 piedi su ciascun estremo (vedi figura 11). 

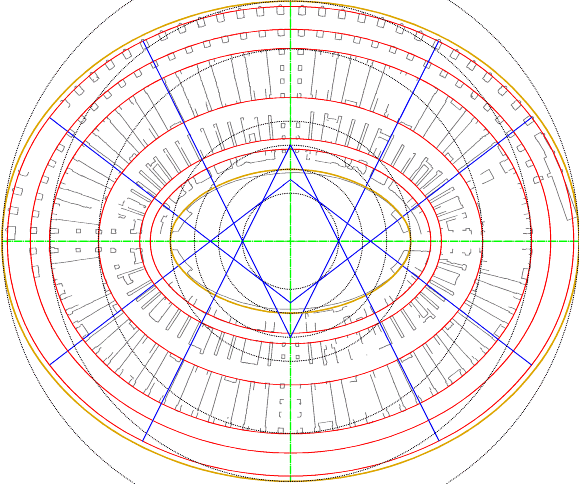
Figura 11
Colosseo. Schema proporzionale basato sul modulo di scala. I semiassi lordi sono di 324 e 270 piedi (rapporto 6/5). Da notare la probabile curva dell’arena, non coincidente con gli ipogei.

Riferendosi ad un elemento più affine agli ipogei che alla cavea e comunque apparendo evidentemente non coerente con le altre, è stata pertanto scorporata dalle compensazioni complessive.

Infine, gli scarti indicano l’ovale a 4 centri come curva interpolante poco probabile – anche per le posizioni che assumono gruppi omogenei di punti di controllo rispetto alla curva stessa, come si è già detto – mentre gli scarti delle ellissi, equidistanti tra loro sugli assi, e degli ovali a 8 centri sono molto simili e verosimili. Tuttavia è da notare, nel caso dell’ellisse, un forte aumento degli scarti passando dalla curva più esterna (4.6 cm) all’interna (14.6 cm); mentre gli scarti per l’ovale a 8 centri si mantengono più uniformi. Infatti, come già notato, la differenza tra l’ellisse e l’ovale a 8 centri aumenta sensibilmente con l’aumentare del rapporto tra gli assi: un ulteriore indizio a favore dell’ovale a 8 centri come curva esecutiva.[15]

È ora necessario individuare il più plausibile coefficiente di trasformazione metro/piede romano. In mancanza dei dati relativi all’arena, non più esistente, Heinz-Jurgen Beste[16] fornisce un’indicazione sulle sue probabili misure indicandole pari a 76.12 e 44.07 metri, aumentate come lì descritto di circa 2 metri per lato (misure finali di circa 80 x 48 metri).

Considerando i semiassi ottenuti dall’interpolazione singola dell’ellisse esterna (curva con scarto più basso, ma risultati analoghi si avrebbero usando le misure dell’ovale a 8 centri) e le lunghezze proposte da Beste, si ottiene, con scarti di ±10 cm, un coefficiente di trasformazione di 29.673 e si individuano le seguenti misure degli assi:

Asse maggiore anfiteatro            636 piedi

Asse minore anfiteatro               528 piedi

Asse maggiore arena                 270 piedi

Asse minore arena                    162 piedi (rapporto 5/3)

Queste misure, con tutta evidenza, indicano un triangolo generatore con rapporti tra i lati 3:4:5; un coefficiente di scala 27 e, dunque, lati di 81, 108 e 135 piedi.

Se questo è il triangolo generatore, il raggio minore dell’ovale a 4 centri sarà pari a 237 piedi (318-81) e il raggio maggiore 372 piedi (237+135). La (7), considerando il calcolo eseguito sul filo esterno delle semicolonne (raggio 1.5 piedi), usando pertanto raggi aumentati di 1.5 piedi, fornisce il seguente risultato per un quarto del perimetro esterno:

P4 = (13/14 * 238.5) + (9/14 * 373.5) = 461 4/7 e dunque il perimetro sarà 1846 piedi e 2/7. Poiché i quattro ingressi principali risultano più ampi rispetto agli altri di circa un piede e mezzo ciascuno, il perimetro ‘netto’ sarà 1840 piedi, vale a dire un interasse ‘teorico’ a filo esterno di colonna di 23 piedi.

I setti radiali (sia pur con alcune incertezze, concentrate sull’anello interno - ma è necessario notare ancora una volta che una piccolissima deviazione dei setti provoca, data la loro breve lunghezza, una notevole variazione di inclinazione – e a parte i setti cardinali, per evidenti ragioni) sembrano convergere verso due centri, posti a circa 80/82 piedi (sull’asse maggiore) e 108/115 piedi (sull’asse minore) dal centro del Colosseo. Provando a invertire la verifica (vedi figura 12), impostando i centri di convergenza a 81 e 108 piedi, si ottiene in ogni modo una buona interpolazione. 

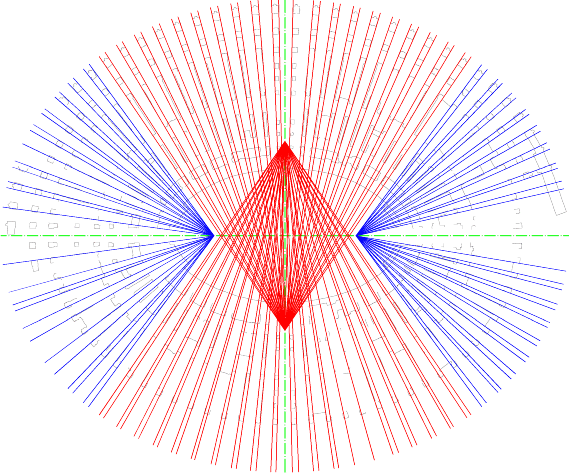
Figura 12
Colosseo. Verifica delle convergenze dei setti interni. I punti di convergenza coincidono con i vertici del triangolo 81:108:135 dell’ovale a 4 centri.

Ma l’ovale a 4 archi, con questi centri, non interpola bene le curve e l’ovale a 8 archi (intestato sul triangolo di quello a 4 centri) nemmeno: in quest’ultimo caso si deve modificare il centro sull’asse maggiore, ponendolo a circa a 90 piedi dal centro del Colosseo, traslandolo dunque di un terzo del modulo di scala rispetto agli 81 piedi originari. In tal modo il raggio minore dell’ovale a 8 centri sarà di 228 piedi (318-90), il raggio maggiore rimarrà 372 piedi e pertanto la loro differenza è di 144 piedi. Ciò significa che il centro dell’arco intermedio si troverà per trilaterazione, usando i due centri principali come basi e 144 piedi come somma delle distanze.

Giunti a questo risultato, rimangono ancora alcune verifiche di grande interesse. Ad esempio, compensando gli insiemi di punti con ovali a 8 centri e imponendo un rapporto prefissato tra le distanze dei due centri principali dal centro dell’ovale (90/108), quale scarto si otterrà? E, soprattutto, le lunghezze dei due lati si porteranno ‘naturalmente’ e autonomamente verso i 90 e i 108 piedi oppure si attesteranno su altre dimensioni? E ancora, tra gli infiniti raggi intermedi ne esiste uno ‘migliore’ e più interessante degli altri, ad esempio nelle proporzioni tra le ampiezze degli archi di cerchio?

La prima domanda trova prontamente una risposta molto positiva. Infatti, imponendo ai lati quel rapporto si ottengono - con uno scarto quadratico medio di 9.7 centimetri, ancora leggermente inferiore allo scarto delle ellissi -, degli ovali interpolanti i quali, una volta scalati i lati dei triangoli generatori a 90 e 108 piedi (vedi figura 13), assegnano al semiasse maggiore una lunghezza di 318.12 piedi e 263.96 piedi al minore: rispetto alle misure ideali, una differenza di tre centimetri e mezzo sul semiasse maggiore e un centimetro sul minore (altri rapporti imposti, scalando poi il cateto ‘fisso’ a 108 piedi, portano ad altri valori per gli assi, spesso molto diversi da quelli appena detti).

Figura 13
Colosseo. Schema finale dell’ovale a 8 centri.

Ma la caratteristica più sorprendente di quei triangoli è ottenuta con una lieve variazione, che sostanzialmente non modifica lo scarto: ruotando il raggio BF di poco più di un grado lo si porta in perfetta corrispondenza con il centro di una semicolonna, precisamente come il raggio AG; ma, soprattutto, il segmento OC risulta allora di 54 piedi precisi, esattamente la metà dei 108 del cateto maggiore e il doppio del modulo di scala, e il segmento OE è vicino ai 67.5 piedi (68.5), prefigurando dunque due triangoli assai peculiari: il primo con rapporto tra i lati 3:4:5 (AEO), l’altro con i cateti nel rapporto 1:2 (BOC).

Inoltre, la distanza AD è circa pari a 72 piedi, la metà di 144, differenza costante tra i raggi. La configurazione ideale (vedi figura 13, in alto a sinistra), con OE pari a 67.5 piedi vede appunto la distanza DA di 72 piedi esatti (il rapporto AE/AD è infatti 25/16).

Infine, un’ultima osservazione sulle proporzioni generali della pianta e dell’alzato del Colosseo. Aumentando di sei piedi i due semiassi, portandoli a 324 e 270 piedi, si giunge al bordo del primo gradino esterno e, soprattutto, ad un rapporto tra gli assi di 6/5. Inoltre, descrivendo cerchi concentrici con passo di 27 e 54 piedi (vedi figura 11) questi scandiscono gli elementi fondamentali della pianta (definendo i rapporti 6/5, 5/4, 4/3, 3/2 e così via), dell’alzato (l’altezza complessiva del Colosseo è pari a circa 162 piedi: 54*3) e dei triangoli generatori (sia degli ovali a 4 sia di quelli a 8 centri). Ed è anche da considerare l’uso della serie proporzionale 3-9-27 e dei suoi derivati. Nel Colosseo – l’unico caso qui disponibile con un rilievo topografico completo degli interni – il modulo di scala sembra allora coincidere con quello proporzionale.

Tabella C.1. Confronto tra gli scarti quadratici medi ottenuti dall’interpolazione dei vari insiemi di punti topografici rilevati nel Colosseo (vedi figure 5..10). Sono presentati i risultati delle compensazioni eseguite contemporaneamente su tutte le curve e quelle compiute su ciascuna curva, separatamente dalle altre. L’ultima colonna si riferisce ad un’interpolazione della curva più esterna, la prima, come ellisse e delle successive come curve parallele alla prima (pertanto non sono ellissi).

Tabella C.2. Confronto tra le lunghezze dei semiassi maggiore e minore per varie curve interpolanti.

Appendice D.  L'Arena di Verona[20]

I dati disponibili si riferiscono al rilievo topografico dell'intera cavea e del profilo dell'arena - parzialmente ristrutturate, però, nel corso dei secoli -, a piante e sezioni di quattro dei settantadue arcovoli ed ai punti perimetrali relativi ai basamenti dei pilastri oggi esterni (vedi figure 14 e 15, quest’ultima tratta dalla ricostruzione del Golvin).

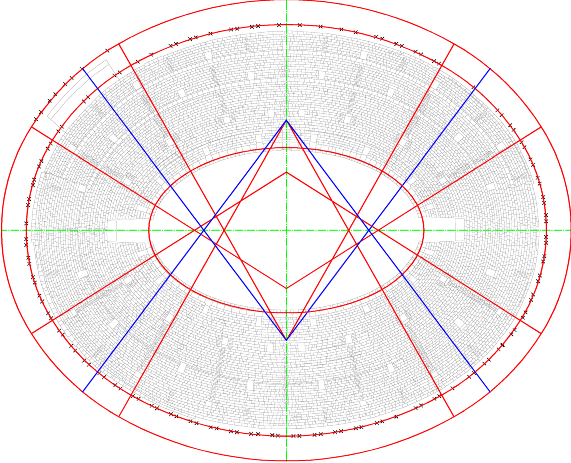
Figura 14
Verona. Rilievo topografico della cavea e della curva esterna e sovrapposizione degli ovali finali a 4 e a 8 centri. Da notare che gli elementi grafici più interni si riferiscono alla pavimentazione dell’arena e non al suo bordo.

Figura 15
Verona. L’anfiteatro di Verona, tratto da J.-C. Golvin, cit., tav. XXXIII.

Le interpolazioni, effettuate sulla sola curva completa dei basamenti esterni, forniscono uno scarto quadratico medio di 15 centimetri per l'ovale a 4 centri, 7.9 centimetri per l'ovale a 8 centri e 7.2 centimetri per l'ellisse (vedi figura 16).[21]

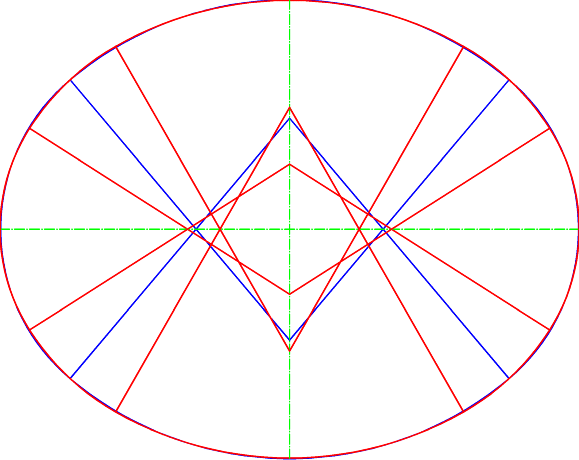
Figura 16
Verona. Sovrapposizione delle curve interpolanti prodotte nella fase di compensazione: ovali a 4 e a 8 centri.

Anche in questo caso, come per il Colosseo, mentre l'ovale a 4 centri non sembra essere candidato come migliore curva interpolante - soprattutto per le caratteristiche delle disposizioni dei punti rispetto alla migliore curva interpolante, simili a quelle del Colosseo -, gli scarti dell'ellisse e dell'ovale a 8 centri sono assai simili, rendendo impossibile stabilire per questa via la genesi geometrica dell'anfiteatro.

Tuttavia, le due curve con scarto minore identificano le lunghezze dei due semiassi in 69.65/54.97 metri (ellisse) e 69.60/55.06 (ovale a 8 centri). Poiché la distanza media dei punti più esterni dalle due curve interpolanti è di 6.7 metri, è possibile stabilire le lunghezze dei due semiassi sul perimetro originariamente più esterno: circa 76.33 e 61.72 metri.

Per quanto riguarda le dimensioni dell'arena, l'ellisse interpolante fornisce - con scarto quadratico medio di 4.4 cm - due lunghezze di semiassi pari a 36.83 e 22.16 metri; mentre l'ovale a 8 centri, con scarto quadratico medio di 5.6 cm, produce due semiassi di lunghezza 36.77 e 22.18 metri.

Usando il valore 0.2954 come fattore di conversione metro/piede, si ottengono i seguenti valori, con scarti massimi compresi tra ± 16 centimetri:

Asse maggiore anfiteatro        518 piedi

Asse minore anfiteatro           418 piedi

Asse maggiore arena              250 piedi

Asse minore arena                 150 piedi (rapporto 5/3)

Nell'ipotesi costruttiva il modulo di scala è pertanto 25, generando un triangolo di 75:100:125 piedi. Infatti, stabilito un interasse tra le lesene esterne di 20.5 piedi e un incremento medio sugli archi cardinali di 1.25 piedi (incrementi che appaiono essere diversi tra loro nei quattro ingressi e concentrati sull’asse maggiore), l'uguaglianza proposta è:

(20 1/2 * 18) + 1.25 = 370.25 @ (13/14 * 184.5) + (9/14 * 309.5).[22]

Dunque, il raggio maggiore è di 309 piedi - dal filo esterno della lesena, dove è calcolato il perimetro, si sottrae infatti mezzo piede, pari allo spessore della lesena stessa -, il semiasse minore della cavea è pari a 209 piedi (raggio maggiore - 4M, con M, il modulo di scala, pari a 25); il raggio minore ha una lunghezza di 184 piedi (raggio maggiore - 5M) e il semiasse maggiore è 259 piedi (raggio + 3M).

Infine, nello schema proposto, il vertice del triangolo 3:4:5 posto sul semiasse maggiore è traslato di 1/3 di modulo (8.3333 piedi), identificando l'ovale a 8 centri che interpola i punti topografici rilevati con uno scarto quadratico medio di circa 8 centimetri (vedi figura 14).

In questo senso, una interessante conferma è descritta nella tabella D.1. I punti relativi alla curva completa sono stati interpolati con un ovale a 8 centri, imponendo però vari rapporti tra i cateti e verificando i valori finali dei cateti stessi e dei semiassi e lo scarto quadratico medio risultante. Imponendo un rapporto di 5/6 (0.83333) tra i cateti - seguendo lo schema proposto, che prevede la traslazione di un terzo di modulo di un vertice - non solo lo scarto risulta in assoluto più basso, sia pur di poco, rispetto ad interpolazioni basate su altri possibili rapporti imposti; ma, soprattutto, i due cateti e i due assi si portano spontaneamente verso i valori previsti: 83.3333 e 100 piedi per i cateti; 518 e 418 piedi per i due assi completi.[23]

Tabella D.1. Confronto tra ovali a 8 centri ottenuti imponendo il rapporto tra i cateti posti sugli assi. Misure in piedi romani.

Appendice E.  Ipotesi su altri anfiteatri con rapporto tra le lunghezze degli assi dell’arena di 5/3

Per una ulteriore pur se ancora limitata verifica, si è studiata l’ipotesi proposta in altri tre anfiteatri probabilmente impostati sullo stesso triangolo. Tuttavia, è necessario osservare che le varie fonti riportano misure spesso assai diverse tra loro, richiedendo dunque un ulteriore esame, compiuto però sulla base di accurati rilievi topografici. I rilievi disponibili, tra l’altro, non chiariscono definitivamente la vera forma dell’anfiteatro, valere a dire se questa sia ellittica oppure ovale, ed in quest’ultimo caso se si tratti di ovali a 4 oppure a 8 centri.

Capua

Misure rilevate[24] espresse in metri e convertite in piedi romani usando il coefficiente di trasformazione di un piede romano pari a 29.665 cm (vedi figura 17).

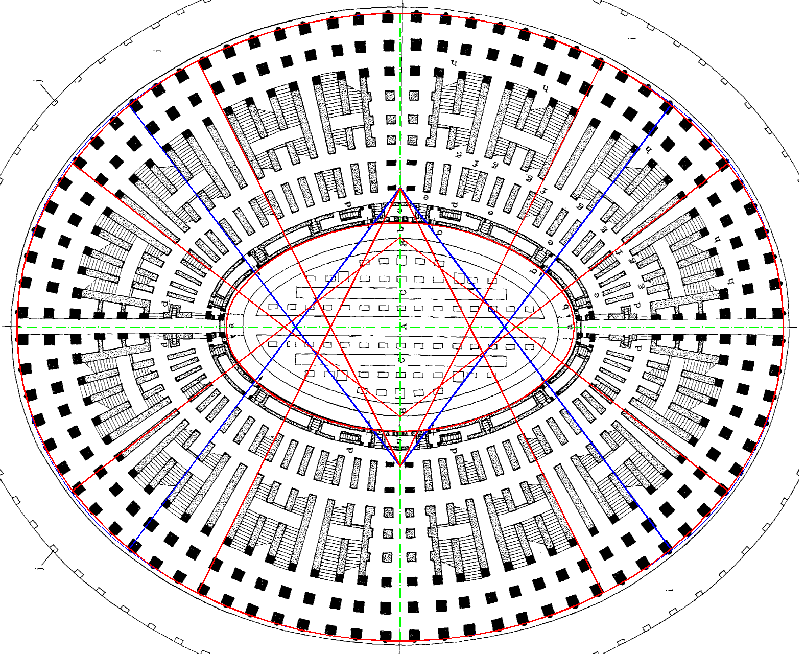
Figura 17
L’anfiteatro di Capua, tratto da J.-C. Golvin, cit., tav. XL.
In colore rosso l’ovale a 8 centri, in blu l’ovale a 4 centri. Per l’indicazione dei valori numerici si veda la tabella E.1.

Lunghezza totale = 166.5 metri = 561.27 piedi;

Larghezza totale = 136.7 metri = 460.81 piedi;

Lunghezza arena = 75.5 metri = 254.51 piedi;

Larghezza arena = 45.7 metri = 154.05 piedi.

Arrotondando e modificando leggermente le misure in 562, 460, 255 e 153 piedi, si prefigura una differenza tra i semiassi di 51 piedi e, pertanto, un modulo di scala di 25 1/2. Questo comporta un triangolo 3:4:5, con lati 76 1/2 : 102 : 127 1/2 piedi.

Tuttavia - in questo caso, per la presenza di un modulo di scala non intero - è possibile che le misure siano state arrotondate a 77:102:127 piedi, portando gli assi dell’arena a 254 e 154 piedi. Queste misure, però, danno una differenza tra i semiassi di 50 piedi e perciò producono due lunghezze di 560 e 460 piedi per gli assi dell’anfiteatro (più vicine alle dimensioni indicate da Wilson Jones) ed un modulo di scala di 25, non direttamente compatibile con le dimensioni dell’arena. Insomma, la mancanza di dati precisi ed attendibili rende quasi impossibile stabilire il grado di ammissibilità delle varie ipotesi.

Per quanto riguarda il calcolo del perimetro, se, come suggerisce Wilson Jones[25], l’interasse di 20 piedi è calcolato al centro del pilastro esterno, circa a 2 piedi dal limite, assumendo quindi il raggio minore pari a 202 1/2 e il raggio maggiore pari a 330 piedi (anziché 204 1/2 e 332), la (7) diviene: P4 = (13/14 * 202 1/2) + ( 9/14 * 330) = 188 1/28 + 212 1/7 = 400 piedi e 5/28.

Il perimetro totale è così pari a 1600 piedi e 5/7, distribuito in 80 archi, tra i quali non sembrano esserci aumenti di larghezza in corrispondenza degli assi cardinali.

Calcolando invece l’interasse sul filo esterno delle semicolonne, aumentando allora di 1 piede le misure date, la (7) diviene:

P4 = (13/14 * 205.5) + ( 9/14 * 333) = 190 23/28 + 214 1/14 = 404 piedi e 25/28.

Il perimetro totale è perciò pari a 1619 piedi e 4/7, vale a dire ottanta archi con interasse di 20 piedi e un quarto[26] (20 1/4 * 80 = 1620 piedi), senza aumenti di larghezza negli archi posti sugli assi di simmetria.

Nell’ipotesi in esame, la curva finale è un ovale a 8 centri, nel quale i due centri principali si trovano a 85 (76 1/2 + 8 1/2, un terzo di 25 1/2) e 102 piedi. Il raggio minore diviene dunque pari a 196 piedi e la differenza rispetto al raggio maggiore (332 piedi) è di 136 piedi, da usare per la trilaterazione che individuerà il centro dell’arco intermedio.

Thysdrus (El-Jem, Tunisia)

Misure rilevate[27] espresse in metri e trasformate in piedi romani adottando il coefficiente di trasformazione di un piede romano pari a 29.355 cm (vedi figura 18).

Figura 18
L’anfiteatro di Thysdrus, tratto da J.-C. Golvin, cit., tav. XLV.
In colore rosso l’ovale a 8 centri, in blu l’ovale a 4 centri. Per l’indicazione dei valori numerici si veda la tabella E.1.

Lunghezza totale = 147.9 metri = 503.84 (504) piedi;

Larghezza totale = 122.2 metri = 416.29 (416) piedi;

Lunghezza arena = 64.5 metri = 219.73 (220) piedi;

Larghezza arena = 38.8 metri = 132.18 (132) piedi.

La differenza tra i semiassi è di 44 piedi (252-208) e pertanto il modulo di scala è 22. Poiché l’arena ha semiassi di 110 e 66 piedi, il triangolo generatore dell’ovale a 4 centri ha la proporzione 3:4:5, con lati 66:88:110 piedi, come del resto propongono anche Golvin[28] e Wilson Jones.[29]

Il raggio minore è pari a 186 piedi (252-66) e il raggio maggiore è di 296 piedi (186+110).

Dunque, per la (7) un quarto del perimetro è pari a:

P4 = (13/14 * 186) + ( 9/14 * 296) = (172 + 5/7) + (190 + 2/7) = 363 piedi.

L’intero perimetro è pari a 1452 piedi: poiché gli ingressi posti lungo gli assi principali sono più larghi di circa 6 piedi ciascuno, il perimetro netto è 1440 piedi, vale a dire 22 1/2 piedi[30] per arco (22 1/2 * 64 = 1440).

Adottando invece, come suggerisce Hedi Slim, il cubito punico di circa 50 centimetri[31] (qui con coefficiente di trasformazione di 49.67 cm), si ottiene:

Lunghezza totale = 298 cubiti;

Larghezza totale = 246 cubiti;

Lunghezza arena = 130 cubiti;

Larghezza arena = 78 cubiti.

Il modulo di scala diviene 13 ((149-123)/2), mentre il triangolo generatore 3:4:5 avrà lati 39:52:65 cubiti. Il raggio minore è di 110 e il maggiore di 175 cubiti.

La (7) porta, per il calcolo del quarto del perimetro, al seguente risultato:

P4 = (13/14 * 110) + ( 9/14 * 175) = 102 1/7 + 112 1/2 = 214 + 9/14. Il perimetro totale è 858 cubiti e 4/7, fornendo un passo di 13.3 cubiti e un aumento in larghezza, per gli ingressi principali, di circa 3 cubiti e due terzi.

Osservando la figura 18, l’ovale a 4 centri appare più verosimile e puntuale dell’ovale a 8 centri: supponendo esatto il rilievo proposto, questo potrebbe semplicemente significare che la seconda fase è stata del tutto omessa, mantenendo anche nella fase esecutiva la forma dell’ovale usato per il progetto. D’altra parte, in questo caso, avremmo un’interessante conferma sull’uso dell’ovale anziché dell’ellisse, molto più vicina all’ovale a 8 centri che all’altro.

Pola

Misure rilevate[32] espresse in metri e tradotte in piedi romani, adottando il coefficiente di trasformazione di un piede romano pari a 29.57 cm (vedi figura 19).

Figura 19
L’anfiteatro di Pola, tratto da J.-C. Golvin, cit., tav. XXXII.
In colore rosso l’ovale a 8 centri, in blu l’ovale a 4 centri. Per l’indicazione dei valori numerici si veda la tabella E.1.  

Lunghezza totale = 123 metri (I fase), 132.5 metri (II fase), 415.97 (416) piedi e 448.09 (448) piedi;

Larghezza totale = 96.5 metri (I fase), 105.1 metri (II fase), 326.35 (326) piedi e 355.43 (356) piedi;

Lunghezza arena = 67.9 metri (I e II fase), 229.63 (230) piedi;

Larghezza arena = 41.7 metri (I e II fase), 141.02 (141) piedi.

I dati sono molto discordanti, poiché la differenza tra gli assi dell’arena è 89 piedi, quella tra gli assi totali della I fase è 90 piedi, mentre nella II fase sale a 92 piedi. Assumendo quest’ultima come base di partenza, il progetto ‘ideale’ potrebbe dunque prevedere 23 come modulo di scala e pertanto un triangolo generatore 3:4:5 con lati 69:92:115 piedi.

L’arena dovrebbe avere assi di lunghezza pari a 230 e 138 piedi (anziché 141).

Infine, in questa ipotesi, la (7) fornisce:

P4 = (13/14 * 155) + ( 9/14 * 270) = (143 + 13/14) + (173 + 4/7) = 317 1/2 piedi. Il perimetro totale è di 1270 piedi, dal quale, sottraendo 5 piedi per ciascuno dei due ingressi principali, si ottiene: 1260 = 72 * 17 1/2 piedi.

Tabella E.1. Confronto riassuntivo dei principali parametri di alcuni anfiteatri verosimilmente impostati sul triangolo 3:4:5. Misure espresse in piedi romani, ricavate dall’applicazione dell’ipotesi proposta.