Le
proporzioni nascoste
nel trait della trompe di
Anet
Camillo Trevisan
email: trevisan@iuav.it
Istituto
Universitario di Architettura di Venezia
Dipartimento di Progettazione Architettonica
Articolo nel
formato PDF (840 kB) ![]()
Questo testo si
riferisce ad un articolo pubblicato in
Disegnare idee e immagini, n. 16 (1999)
Data crezione: giugno 1999
Migliore vista con Internet Explorer 4 o versioni
superiori,
Netscape 4 o versioni superiori, risoluzione 1024x768,
con dimensioni medie del carattere.
Philippe de La Hire fornisce la più semplice
spiegazione del significato del termine trait:
"Gli operai chiamano la scienza del trait, nel
taglio della pietra, quella che insegna a tagliare e
costruire separatamente più conci di pietra, in modo
tale che, quando sono opportunamente composti assieme,
questi costituiscono un manufatto che può considerarsi
come un tutt'uno."1
Il trait è dunque un grafico, di norma tracciato
in scala, che permette di risolvere problemi costruttivi
reali, legati alla conformazione e al taglio di conci di
pietra.2
In questo campo uno dei primi trattatisti è stato
Philibert Delorme3,
il quale illustra, tra l'altro, le modalità di
definizione dei trait 4
relativi alla trompe 5
di Anet (figure 1-5).
Questo piccolo cabinet - costruito attorno alla
metà del Cinquecento nel castello di Diane de Poitiers e
ormai distrutto - sarà ripreso da molti trattatisti
successivi come paradigma e modello di costruzione
complessa e ardita.
Il metodo geometrico del trait ideato da Delorme,
apparentemente farraginoso e oscuro, è in realtà di
assai semplice applicazione (figura
6). Per mezzo di rotazioni e ribaltamenti, a partire
da una pianta e da una sezione verticale, consente di
definire - nelle due dimensioni del grafico - l'altezza
di ciascun punto del manufatto e, pertanto, la curva di
intersezione tra due superfici. Inoltre, sempre
attraverso le stesse operazioni, permette di costruire i cartoni
di sviluppo (panneaux) della superficie inferiore
e superiore della volta e del suo fronte. In tal modo,
non solo si potranno facilmente costruire modelli in
cartone o gesso, ma si potrà anche procedere
operativamente al taglio dei conci di pietra.
Per il taglio, infatti, si possono adottare due
procedimenti principali: par équarrissement
e par panneaux.
Nel primo caso, d'origine assai lontana nel tempo, si
utilizzano le proiezioni ortogonali del concio, di norma
di forma assai semplice.
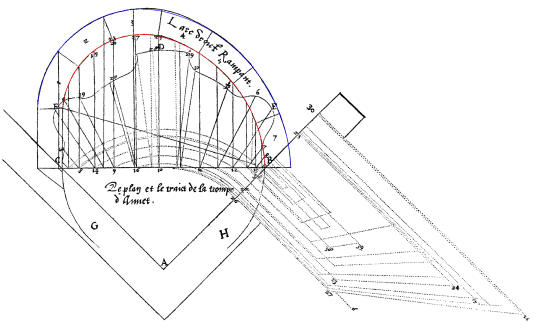

Figura 2 (a sinistra). Delorme, cit., f. 92v.-93r. Trait usato per la costruzione dei cartoni della trompe di Anet. In colore, per confronto, sono evidenziati gli ovali ottenuti mediante la costruzione presentata nell'articolo.
In colore, per confronto, sono evidenziati gli ovali ottenuti mediante la costruzione presentata nell'articolo.
Nel trattato i grafici sono tutti alla stessa scala.
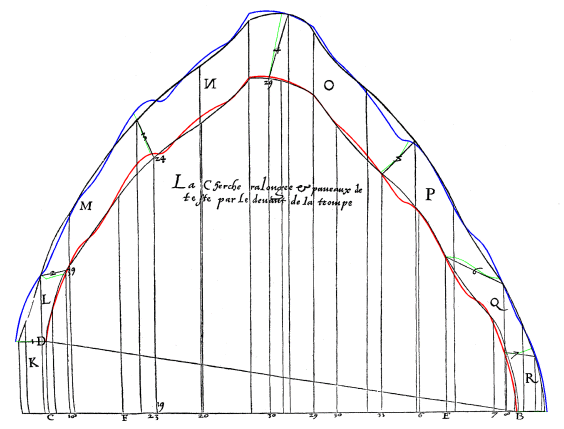
Figura 4 (in basso a destra). Delorme, cit., f. 95v. Cartone dello sviluppo della volta inferiore della trompe di Anet. In colore, per confronto, sono evidenziate le costruzioni ottenute mediante l'uso del programma Trompe (il programma, di uso gratuito e reperibile nella pagina trompe.htm, consente di produrre il modello tridimensionale a facce e i cartoni di sviluppo di una generica trompe conica, a partire dal trait).
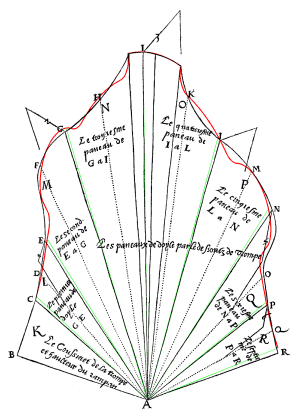
Figura 5 (in basso a sinistra).
Delorme, cit., f. 94v. Cartone dello sviluppo frontale
della trompe di Anet.
In colore, per confronto, sono evidenziate le costruzioni
ottenute mediante l'uso del programma Trompe.
Da notare, come anche nell'immagine precedente, le
sovrapposizioni nei punti certamente calcolati da
Delorme.
Il metodo par panneaux prevede invece di ricavare ciascuna faccia del concio a partire da un'altra, ad essa adiacente, conoscendo l'angolo tra le due facce e, nel caso di superfici curve, il modano che definisce la curvatura.6
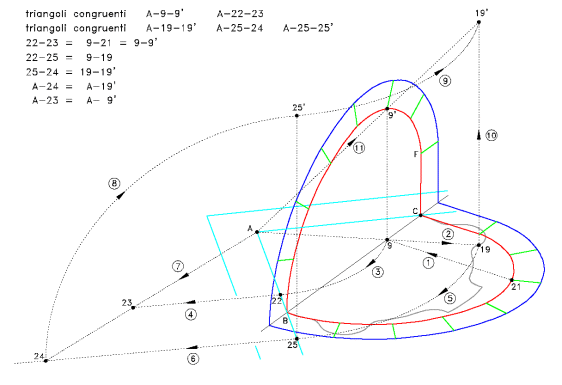
Lo schema qui riportato riproduce, nelle tre dimensioni, le operazioni geometriche bidimensionali adoperate dallo stesso Delorme nel suo trattato (vedi figura 2). In rosso è indicata la sezione dell'intradosso; in blu quella dell'estradosso; in verde sono indicati i giunti tra i conci.
I metodi della stereotomia - così come, ad esempio, quelli della statica grafica - richiedono dunque una fortissima sintonia tra fase progettuale ed esecutiva.
Il trait non può in alcun modo costituire una semplice dichiarazione d'intenti; di essenza prettamente ideologica e con la possibilità di ampie correzioni in corso d'opera. Al contrario, ogni minimo spostamento del più piccolo segmento si riverbererà sull'edificio amplificato più volte e con ripercussioni, in alcuni casi critiche, sulla sua stessa stabilità.
In questa sede l'attenzione è focalizzata sulla ricerca delle proporzioni tra gli elementi grafici del trait principale. Quest'ultimo, infatti, rappresenta una sezione verticale del manufatto e pertanto ne definisce completamente i rapporti tra le parti.
Cercare le proporzioni nel grafico, equivale dunque allo studio proporzionale compiuto sull'edificio stesso: analisi, in questo caso, ormai impossibile; ma ricerca non impertinente, tuttavia, visto il proposito dello stesso Delorme di scrivere un Second Tome de l'Architecture, tutto dedicato allo studio delle proporzioni.7
Il
trait della trompe
di Anet
La ricerca intrapresa può essere suddivisa in alcuni
passaggi essenziali:
- identificazione della forma geometrica della sezione
verticale ribaltata, per definire se questa è ovale o
ellittica;
- indagine sulle proporzioni geometriche riferite al trait;
- verifica della reciproca coerenza dei grafici
presentati nel trattato di Delorme;
- definizione della grandezza del manufatto e del
rapporto di riduzione dei grafici, sulla scorta dei
documenti disponibili.
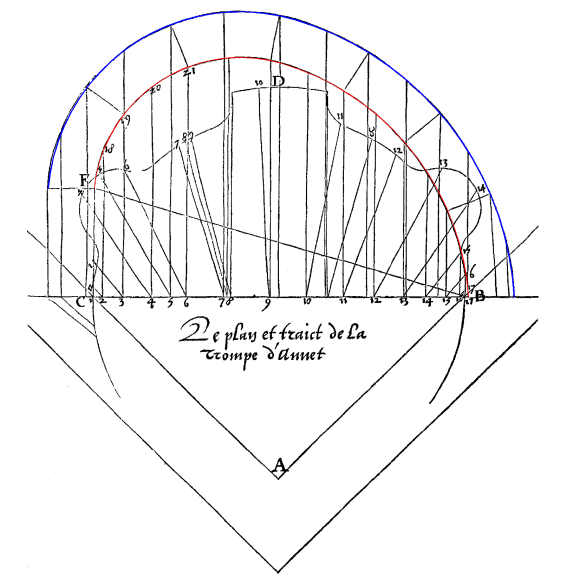
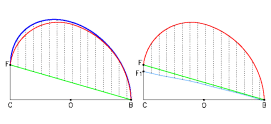
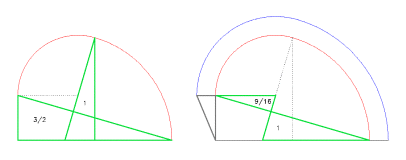
Robin Evans propone che la curva principale del trait sia una semiellisse asimmetrica, generata facendo slittare le corde verticali di un semicerchio, costruito sulla base, fino al loro punto di intersezione con la retta inclinata: la rampa della trompe (figura 7).8 Il procedimento, tuttavia, pur se ingegnoso ed elegante (del resto illustrato anche da De La Ruë 9), non produce però la curva disegnata nel trait della trompe di Anet, né una vera ellisse.
La curva realmente usata (grafico a destra), seguendo lo stesso procedimento al contrario, conduce però alla retta BF1 (in realtà una spezzata molto vicina ad una retta). Come si può notare, la differenza è di non lieve entità e certamente superiore all'errore dell'incisore.
Figura 8 (in basso). Costruzione dell'arco rampante proposta da De La Ruë. Definita la base AB, la rampa AD ed un segmento verticale dal punto medio di AB, si pone LK uguale ad LB. Trovato il punto di mezzo E di BK, si reperisce il punto F, centro dell'arco G da B a K, e successivamente il punto I, centro dell'arco H da D a K. In tal modo i due centri sono allineati con il punto di giunzione K. In figura sono state usate le stesse lettere indicate dall'autore.

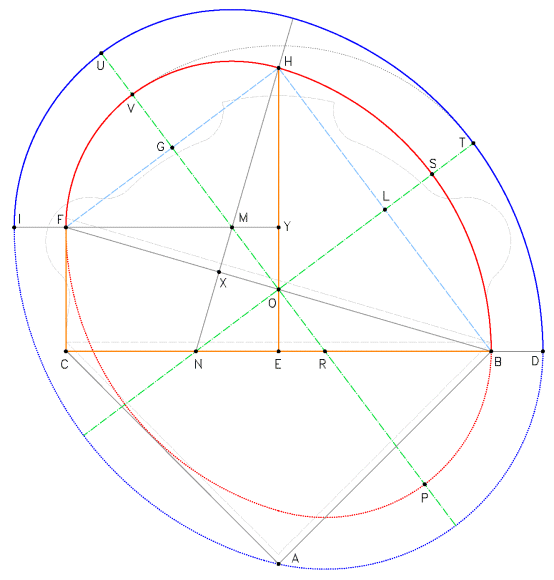
I triangoli EHB e FYH sono triangoli rettangoli perfetti 3-4-5. Il semiasse minore dell'ovale esterno è congruente al semiasse maggiore dell'ovale interno. In linea tratteggiata di colore grigio è indicata la pianta della trompe, traslata di 1/6 di piede rispetto alla base originale CB.
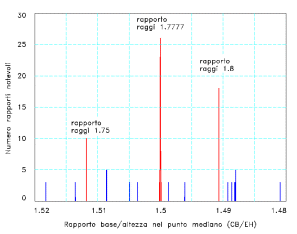
Figura 10 (in basso). Grafico che mostra il numero di rapporti notevoli instaurati tra i segmenti principali del trait, al variare del rapporto tra base e altezza dell'ovale interno. L'ovale preso in esame nell'articolo si riferisce ad un rapporto tra base e altezza pari a 1.5 (EH = 2/3 CB).
Supporre che la curva generatrice sia un ovale piuttosto che un'ellisse, tiene dunque conto della facilità di costruzione dell'ovale e, soprattutto, di conci con superfici a sezione circolare anziché ellittica; ed infine, di analoghi esempi riferiti all'arco rampante.
Tuttavia, data la piccola differenza esistente tra un'ellisse ed un ovale (la distanza massima tra le due curve è, in questo caso, inferiore allo 0.4% dell'asse maggiore), questi argomenti, pur solidi, non sono sufficienti per stabilire inequivocabilmente la forma della curva. È necessaria una riprova decisiva, basata non solo sul confronto diretto - non conclusivo né univoco - ma anche su riscontri teorici, geometrici e matematici: in breve, sulla proporzione.
La forma
geometrica della sezione verticale
I segmenti sui quali si fonda tutta la costruzione della trompe
sono evidentemente la base, l'altezza della volta nel
punto mediano e l'altezza della rampa (segmenti BC, EH e
CF della figura 9). La base stabilisce l'ampiezza della
pianta ed anche le lunghezze dei lati di sostegno che
confluiscono nel vertice A; il secondo segmento definisce
l'altezza della volta; il terzo, legato ai primi due,
indica di quanto la volta sarà rampante.11
Essi definiscono pertanto i limiti della figura di
costruzione e dunque la forma della superficie inferiore,
l'intradosso della volta rampante.12
Il metodo illustrato da De La Ruë (figura 8), produce
infiniti ovali diversi tra loro, tutti caratterizzati -
qualunque sia il rapporto tra base e altezza - da
numerose proporzioni geometriche, aritmetiche e armoniche
ricorrenti tra i segmenti costruttivi; tutte esatte,
vale a dire con scarto tra i rapporti o le differenze
pari a zero (cfr. tabelle 2,
3, 4).

È l'ovale basato sui triangoli rettangoli perfetti 14, principalmente sul triangolo con proporzioni tra i lati di 3-4-5.15
Definita una base BC (figura 9) e trovato il suo punto di mezzo E, s'imposta un primo triangolo 3-4-5 con il suo cateto minore pari a EB, metà della base. Il cateto maggiore EH è dunque pari a 4/3 di EB o anche 2/3 di BC. Un secondo triangolo 3-4-5 avrà invece il cateto maggiore della stessa lunghezza EB ed un vertice in H (figura 11.1).
Questa semplice operazione definisce completamente l'ovale interno, trovando la rampa CF per differenza; costruendo allo stesso tempo una ricca serie di altri triangoli simili (figura 11).
L'ovale esterno (l'estradosso della volta) si troverà facilmente ponendo la lunghezza del suo semiasse minore pari a quella del semiasse maggiore dell'ovale interno.16
Anche altri triangoli rettangoli definiti nel trait sono assai singolari (BCF, NEH, NXB e MXF, nella figura 9). Le lunghezze dei lati di questi triangoli, infatti, formano anch'esse una tripletta pitagorica con sequenza proporzionale a 7-24-25. I quattro triangoli definiscono, circolarmente, i legami fondamentali esistenti tra base e rampa; tra raggio maggiore e altezza e tra i due raggi dell'ovale e la base stessa (figura 12).
Infine, il triangolo CFI - a sua volta derivato dalla rampa e dalla differenza tra i semiassi dell'ovale - è ancora un triangolo rettangolo perfetto, con sequenza proporzionale a 5-12-13 (figura 12.2).
In questo grafico costruttivo, pertanto, i primi tre triangoli rettangoli perfetti sono tutti presenti e legati strettamente tra loro in un fittissimo intreccio di relazioni e di proporzioni.
Tessitura che è impossibile definire casuale, soprattutto se si tiene conto della piena sovrapposizione dei due ovali con entrambi gli esempi tracciati sul trattato17, sia pur con le leggere imperfezioni di una xilografia (figure 2 e 3).
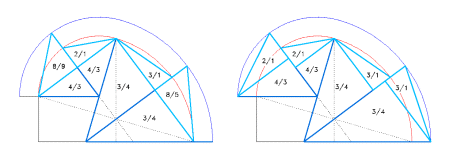
Come ulteriore conferma, i triangoli 3-4-5 - impostati con le loro ipotenuse sui raggi degli ovali interno ed esterno - sono in stretta relazione con altrettanti triangoli rettangoli, aventi un cateto in comune e l'altro cateto che completa le lunghezze dei semiassi (figura 13).
Questi ultimi triangoli hanno i loro cateti nel rapporto di 2/1, per il semiasse maggiore, e di 3/1, per il semiasse minore.
Il raggio del cerchio inscritto, indicato per i triangoli più grandi, è pari a un terzo del lato minore del triangolo. Da notare le sequenze di rapporti che legano i lati dei vari triangoli e questi ultimi ai segmenti fondamentali del trait e agli altri triangoli perfetti, con rapporti 7-24-25 e 5-12-13.
Figura 12 (in basso, a sinistra). Identificazione di alcuni triangoli rettangoli perfetti, con rapporti tra i lati di 7-24-25 (in colore verde) e 5-12-13 (grigio). Da notare, come anche nel caso dei triangoli 3-4-5, le sequenze di rapporti che legano i lati dei vari triangoli e questi ultimi ai segmenti fondamentali del trait.
Figura 13 (in basso, a destra). Relazioni esistenti tra i triangoli 3-4-5, impostati con la loro ipotenusa sui raggi degli ovali interno ed esterno, ed i segmenti che completano i semiassi degli ovali interno ed esterno.

In particolare, oltre a tutte le relazioni date direttamente dai triangoli rettangoli perfetti, sono significative anche le numerose proporzioni aritmetiche e armoniche caratteristiche solo di quella coppia di ovali (cfr. tabelle 3 e 4).
Definizione delle dimensioni
della trompe e del rapporto di scala
nelle rappresentazioni
Dopo aver classificato come ovale la forma geometrica
della figura; avendo identificato il metodo di
costruzione grafica; definiti i centri e i raggi di
costruzione e verificata la sovrapposizione degli ovali
con i grafici originali, è ora interessante stabilire la
dimensione della costruzione e la scala di
rappresentazione.
Un disegno, identificato da Anthony Blunt18, mostra la facciata
occidentale dell'ala Est del castello di Anet con una
vista in proiezione ortogonale della trompe dal
lato non rampante. Da quel disegno si può ricavare la
misura del lato, pari a circa 5.2 piedi, mentre l'altezza
della volta rampante è di circa 10 piedi.19
Un altro indizio proviene dallo stesso Delorme: in un
passo del suo trattato egli afferma che la lunghezza del
concio massimo è di 10/12 piedi.20
Questi due dati costituiscono dunque l'insieme, in
verità assai ridotto, delle indicazioni in nostro
possesso per stabilire le dimensioni della trompe.
Dimensioni che, prendendo come riferimento la base BC,
possono pertanto variare tra 5.8 piedi (per una lunghezza
del concio massimo di 10 piedi) e 7.4 piedi (per un lato
di circa 5.2 piedi).21
Tuttavia, mantenendo fisse le proporzioni degli ovali
(ormai definitivamente identificate), ma variando la
scala, si generano lunghezze via via diverse per i
segmenti fondamentali del trait e valori diversi
per le proporzioni aritmetiche e armoniche. Anche in
questo caso, scandagliando un gran numero di possibili
dimensioni della trompe, si perviene
all'identificazione di un preciso valore, candidato ad
essere scelto come quello realmente usato per la
costruzione (figura 14 e
tabella 1).22
Fissando la grandezza della base CB a 7 piedi e 1/5,
l'altezza della volta risulta essere di 10 piedi esatti e
il lato di circa 5.1 piedi, valori assolutamente
concordanti con i dati in nostro possesso.23
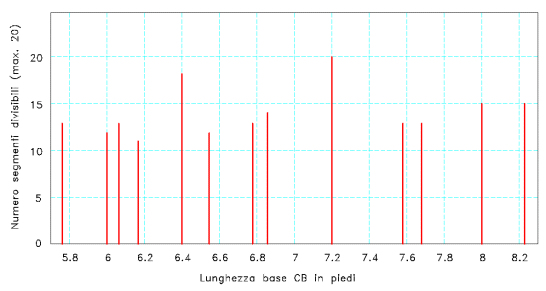
Per riferimento, in ascissa è indicata la lunghezza della base CB. In un largo intorno, solo una base pari a 7.2 piedi fa sì che siano divisibili in frazioni tutti i segmenti fondamentali della coppia di ovali presi in esame.
Nel grafico sono mostrati solo i valori delle basi che producono più di 10 segmenti divisibili in frazioni.
Figura 15 (a destra). Assonometria ortogonale
dimetrica della trompe di Anet.
Rendering eseguito sul modello tridimensionale a facce
prodotto dal programma Trompe.
A tale riguardo è da notare che, nel suo trattato, Delorme riporta in scala naturale le grandezze del piede e del palmo romano e del piede francese.24
Inoltre, a meno di piccole variazioni dovute al metodo xilografico di stampa25, i grafici - le due piante, lo sviluppo frontale e quello dell'intradosso - sono tutti alla stessa scala: ad un piede nella realtà corrispondono 2/3 di pollice sul disegno (rapporto di riduzione 1:18).
Questo dato, pertanto, conferma ulteriormente e rafforza la tesi che indica in 7.2 piedi (una tesa e 1/5) la grandezza della base costruttiva dell'intero trait.
Conclusioni
L'uso del trait géométrique agisce sull'edificio
come una leva progettuale, moltiplicando le azioni
in una reazione a catena che ci lascia stupefatti.
Pochi tratti, in questo caso due semplici archi di
cerchio, regolano e definiscono l'intera architettura,
trasmettendole per partenogenesi tutti i caratteri, le
proporzioni, le volumetrie potenziali.
L'atto creativo progettuale, infatti, risiede
completamente nella costruzione del trait: è
un'azione indiretta, dunque, e non riguarda l'oggetto in
sé ma le sue sezioni costruttive.
In tal senso, non ci sorprende lo stupore e l'entusiasmo
dello stesso Delorme quando ne descrive le
caratteristiche e gli effetti meravigliosi.
Se a tutto questo aggiungiamo la possibilità immediata
di generare modelli tridimensionali e di controllare,
passo dopo passo, la costruzione reale, il metodo del trait
doveva certamente apparire come una novità
rivoluzionaria.
L'aspetto forse più interessante, nello studio delle
proporzioni di questi grafici, sembra dunque essere
proprio il tentativo di giungere a scandagliare lo stadio
primitivo del concepimento dell'architettura.
Lato piedi frazioni
IF 7/8
OM 1 5/16
NE 1 2/5
NO 1 3/4
CF 2 1/10
NM 2 3/16
CN 2 1/5
YH 2 7/10
MH 2 13/16
OS 3 1/4
CE 3 3/5
MU 3 11/16
OV 4 1/8
FH 4 1/2
EH 4 4/5
NH 5
OU 5
NT 5 7/8
HB 6
CB 7 1/5
FB 7 1/2
Numeratori:
1, 2, 3, 4, 5, 7, 11, 13
Denominatori:
2, 4, 5, 8, 10, 16
NO/NH = CF/HB = NO/OU 7/20 0.35
MY/NM = YH/FB 9/25 0.36 (1/2.77777)
MY/CF = YH/CB = MH/FB 3/8 0.375 (1/2.66666)
NE/CE = NO/FH 7/18 0.388888
NM/NH = CF/EH = NM/OU 7/16 0.4375
MY/NO = YH/HB 9/20 0.45 (1/2.22222)
OM/MH = CF/FH 7/15 0.466666
IF/NO = CE/CB 1/2 0.5 (1)
YH/EH = MH/NH = MY/NE = MH/OU 9/16 0.5625 (1/1.77777)
MY/OM = OM/NM = YH/FH = FH/FB = CE/HB 3/5 0.6 (2) (1/1.66666)
MH/FH = FH/CB = OM/CF = IF/NE 5/8 0.625 (1/1.6)
NE/NM = EH/FB 16/25 0.64
OS/NH = OS/OU 13/20 0.65
NE/CF = EH/CB = NH/FB = IF/OM = OU/FB 2/3 0.666666 (3) (1/1.5)
OM/NO = YH/CE = CE/EH = FH/HB 3/4 0.75 (2) (1/1.33333)
CF/YH = NM/MH 7/9 0.777777
NE/NO = NO/NM = CE/FH = EH/HB = HB/FB 4/5 0.8 (2)
NH/HB = HB/CB = NO/CF = OU/HB 5/6 0.833333 (1/1.2)
MY/IF = FH/NH = FH/OU 9/10 0.9 (1/1.11111)
OM/NE = FH/EH 15/16 0.9375 (1/1.06666)
YH/MH = EH/NH = CF/NM = CB/FB = EH/OU 24/25 0.96
OV/OT = NH/OU 1/1 1 (4)
In neretto sono indicate le proporzioni o i
rapporti validi solo per l'ovale in esame. Negli altri
ovali, costruiti con lo stesso metodo, valgono tutte le
altre proporzioni, ma con valori diversi da questi.
I valori indicati sono validi per qualsiasi scala.
(1) CE=1/2 CB per
costruzione.
(2) Proporzioni tra i
lati del triangolo pitagorico 3-4-5.
(3) EH=2/3 CB per
costruzione.
(4) OV=OT per
costruzione.
CF-EH = EH-FB -2.7 (216/80, 27/10)
CF-FH = EH-CB -2.4 (192/80, 12/ 5)
OM-CE = WZ-CB = NE-MU -2.2875 (183/80)
NE-CE = NH-CB = OU-CB -2.2 (176/80, 11/ 5)
FH-HB = HB-FB = OM-MH = NO-OS = CF-CE = NM-MU -1.5 (120/80, 3/ 2)
CN-CE = CE-NH = MY-NM = CE-OU -1.4 (112/80, 7/ 5)
IF-CN = NT-CB -1.325 (106/80, 53/40)
MU-NH = IF-NM = MH-OV = CE-WZ = MY-CF = MU-OU -1.3125 (105/80, 21/16)
IF-CF = MU-WZ -1.225 ( 98/80, 49/40)
CE-EH = EH-HB = HB-CB -1.2 ( 96/80, 6/ 5)
MY-NO = WZ-NT -0.9625 ( 77/80)
YH-CE = CE-FH -0.9 ( 72/80, 9/10)
OS-OV=OV-OU=NH-NT = MH-MU = OV-NH = OU-NT = IF-NO = OM-NM -0.875 (1) ( 70/80, 7/ 8)
MH-CE = NE-NM = OM-CF = OV-WZ -0.7875 ( 63/80)
MY-NE = CN-MH -0.6125 ( 49/80)
MY-OM = CE-OV = IF-NE -0.525 ( 42/80, 21/40)
CN-YH = FH-NH = FH-OU -0.5 ( 40/80, 1/ 2)
IF-OM = NO-NM = MU-OV = MH-OS = OS-MU = OM-NO -0.4375 ( 35/80, 7/16)
OS-CE = NE-NO = NO-CF -0.35 ( 28/80, 7/20)
FH-EH = CB-FB -0.3 ( 24/80, 3/10)
YH-MH = EH-WZ -0.1125 ( 9/80)
MY-IF = CE-MU = OM-NE = CF-NM = WZ-NH = WZ-OU -0.0875 ( 7/80)
In neretto sono indicate
le proporzioni valide solo per l'ovale in esame. Negli
altri ovali, costruiti con lo stesso metodo ma con
diversa proporzione tra base e altezza, valgono tutte le
altre proporzioni aritmetiche, anche se con valori
diversi da questi.
Inoltre, tutti i valori presentati in tabella valgono
solo per la scala considerata (base di 7.2 piedi).
In questa tabella compaiono anche i segmenti MY e WZ
(altezza massima dell'ovale sul punto M, somma di CF e
MH).
(1) Le proporzioni in
neretto, in questo caso, sono valide anche per tutti gli
altri ovali, ma con valori diversi una dall'altra.
IF/NM 2/ 5
IF/CF 5/12
NE/CN 7/11
CF/CE 7/12
NO/OS 7/13
CN/OV 8/15
OV/FH 11/12
OV/HB 11/16
CN/CE 11/18
OV/FB 11/20
OS/FH 13/18
1/NH - 1/HB = 1/HB - 1/FB = 1/OU - 1/HB
0.033333 (3/90, 1/30)
1/CE - 1/FH = 1/FH - 1/HB
0.055555 (5/90, 1/18)
1/CE - 1/EH = 1/EH - 1/CB
0.069444 (5/72)
1/MH - 1/CE = 1/CE - 1/NH = 1/CE - 1/OU 0.077777
(7/90)
1/NE - 1/NM = 1/NM - 1/NH = 1/NM - 1/OU
0.257143 (9/35)
In neretto sono indicate le proporzioni
valide solo per l'ovale in esame. Negli altri ovali,
costruiti con lo stesso metodo, valgono tutte le altre
proporzioni armoniche, ma con valori diversi da questi.
Inoltre, tutti i valori presentati in tabella valgono
solo per la scala considerata (base di 7.2 piedi).
1 Philippe de La Hire, Traité de la coupe des pierres, ms. 1596, Paris, Bibliothèque de l'Institut de France, f. 1.
2 Nel sito Internet: http://www.iuav.it/dpa/ricerche/trevisan/stereo/stereo.htm
è consultabile uno studio
sulla stereotomia e la tecnica del trait. La
stereotomia è la scienza del taglio dei solidi; ed usa
le proiezioni geometriche per la determinazione della
forma e delle dimensioni dei conci di pietra che
costituiscono archi, volte o cupole.
Non la semplice preparazione di conci in pietra, dunque,
ma l'insieme di procedure geometriche codificate,
coerenti e ripetibili, atte a progettare ed a
rappresentare interi edifici costruiti in pietra. È
Jacques Curabelle ad usare per la prima volta il
termine stereotomia, nel suo libello del 1644
contro Desargues: Examen des oeuvres du Sieur
Désargues.
3 La prima edizione del trattato di Philibert Delorme è stata pubblicata nel 1567 (Frédéric Morel, Paris), con il titolo di Le Premier Tome de l'Architecture…. Questa prima edizione comprendeva nove libri. A riprova del suo successo, è stata poi ristampata nel 1576-78, 1626, 1648, 1894, in edizioni che comprendevano anche, come libri X e XI, le Nouvelles Inventions pour bien bastir et à petits fraiz… (1a ed. Frédéric Morel, Paris 1561). L'edizione del 1648 (David Ferrand, Rouen) è stata ristampata in riproduzione anastatica nel 1981 a Bruxelles, da Pierre Mardaga. L'edizione del 1567 è stata invece ristampata in anastatica nel 1988, assieme alle Nouvelles Inventions… e con presentazione e commento di Pérouse de Montclos, dall'editore Léonce Laget, Paris.
4 Delorme, nel suo trattato, usa il termine traict anziché trait: si adotterà quest'ultima forma, usata dai trattatisti successivi ed entrata nell'uso corrente.
5 La trompe è una piccola volta - di
norma formata da conci di pietra - che sopporta una
copertura o un muro a strapiombo.
Come tutte le volte o gli archi, la trompe si
sostiene - e regge le opere murarie soprastanti -
scaricando il peso dell'intera struttura sulle imposte.
Questa voûte suspendue en l'air, come la chiama
lo stesso Delorme, era costruita per sorreggere scale o
piccoli cabinet, come nel caso della trompe di
Anet, senza la necessità di poggiarsi a terra; ma forse
soprattutto per ottenere un elemento caratterizzante
l'intero edificio.
6 Esiste anche un terzo metodo, par demi-équarrissement, che fonde i vantaggi pratici dei primi due. In questo caso il concio è tagliato usando sia alcune sue proiezioni frontali, sia alcuni cartoni di sviluppo, modani e angoli definiti tra due facce del concio stesso.
7 "Je n'use d'autres mesures sinon des proportions lesquelles j'ay tirées de l'Escriture saincte du vieil testament et (ce que je diray sans aucune jactance) les mets en usage le premier, ainsi que je feray apparoir de bref, Dieu aydant, par le discours de nostre seconde partie d'architecture, qui porte le titre et nom: Des divines Proportions". Delorme, cit., f. 168r.
8 Robin Evans, La trompe di Anet, in "Eidos", 2 (1988), p. 50-57. Si veda la figura 7. Fissato il segmento di base BC e l'altezza CF (immagine a sinistra), si alzano, a partire da BF, dei segmenti perpendicolari a CB, di lunghezza pari alla loro distanza verticale da BF. Con questa costruzione, come si vede, si ottiene però una curva (quella superiore) che non coincide affatto con quella usata da Delorme come profilo di sezione. La curva realmente usata (grafico a destra), seguendo lo stesso procedimento al contrario, conduce però alla retta BF1 (in realtà una spezzata molto vicina ad una retta). Se si usa l'inclinazione della retta BF indicata sul trait, la curva è dunque troppo alta; oppure, per ottenere una curva simile, l'inclinazione stessa deve essere ridotta di circa 3° (BF1), abbassando di molto il piede verticale rispetto al disegno originale.
9 Tirer un Arc rampant d'un Arc droit. Jean Baptiste De La Ruë, Traité de la coupe des pierres, Imprimerie Royale, Paris 1728, p. 6, tav. I, fig. 9.
10 Décrire l'Arc rampant de deux ouvertures de Compas. Si veda la figura 8. "Sia AD l'altezza della rampa, BD la linea della rampa ed LK la perpendicolare al punto di mezzo di AB. Posto LK uguale a LB, portare, dal punto di mezzo E di BK, la retta EF perpendicolare a KB. Trovato il punto F su AB, tracciate FK e tracciate anche DI, parallela ad AB. In tal modo si troverà il punto I su FK. Dal punto I, e con raggio ID, tracciate l'arco DHK; dal punto F e con raggio FK tracciate l'arco KGB: questi due archi formeranno l'arco rampante DHKGB richiesto". De La Ruë, cit., p. 6, tav. II, fig. 1.
11 Nella figura 9 si può notare che la pianta della trompe è stata traslata da Delorme di 1/6 di piede: in tal modo le tangenti ai due archi nei punti di inizio non sono verticali, ma leggermente inclinate verso l'interno. Aver tagliato la parte bassa dell'ovale fa sì che l'attacco della volta della trompe non sia tangente ai due muri di sostegno. In tal modo non solo si rendono visibili gli spigoli di inizio della volta, ma soprattutto, variando così le altezze, si possono adattare le dimensioni della trompe ai vincoli preesistenti: la finestra da scavalcare sul lato rampante e le altezze dei solai.
12 Pérouse de Montclos propone che la trompe di Anet sia conico sferica, poiché la rappresentazione di quella trompe nel trattato di Delorme mostra, sopra la finestra, un taglio curvo e non rettilineo (cfr. Jean-Marie Pérouse de Montclos, L'architecture à la française, XVIe, XVIIe, XVIIIe siècles, Picard, Paris 1982, p. 94; si veda anche la figura 1). Il trait considerato e illustrato da Delorme è però evidentemente quello di una trompe conica (si veda anche la figura 15). Inoltre, Frézier la tratta anch'egli come trompe conica, quando la trompe è ancora esistente (cfr. Amédée-François Frézier, La théorie et la pratique de la coupe des pierres et des bois…, 3 vol., Strasbourg-Paris 1737-39, Libro IV, p. 265).
13 Si è costruito un programma per computer, in
grado di identificare tutti i possibili rapporti tra i
segmenti principali dell'ovale, al variare del rapporto
tra la base e l'altezza dell'ovale e considerando come
valido un rapporto tra i primi 20 numeri naturali. Nella
figura 10 sono riportati i risultati dell'analisi di
oltre 40 mila ovali, con tale valore variabile tra 1.52 e
1.48: in essa si evidenzia nettamente l'ovale con
rapporto tra base e altezza di 1.5 e rapporto tra i raggi
pari a 1.7 periodico.
È anche da notare che gli altri due ovali, con rapporto
tra i raggi 1.75 e 1.8, si discostano sensibilmente dai
grafici presentati da Delorme nel suo trattato, al
contrario dell'ovale considerato, perfettamente
coincidente con quei grafici.
14 Le relazioni che legano i tre lati L1, L2, L3 di un triangolo rettangolo perfetto sono: L1 = q2 - p2; L2 = 2 p q; L3 = q2 + p2; dove p e q sono due numeri naturali, uno pari e l'altro dispari e con massimo divisore comune pari a 1. Ponendo p=1 e q=2 si ottiene il triangolo con lati di 3, 4, 5 unità; con p=2 e q=3 si costruisce il triangolo 5-12-13; mentre con p=3 e q=4 si trova il triangolo rettangolo 7-24-25.
15 Il triangolo rettangolo con lunghezze dei lati di 3, 4, 5 unità - noto anche come triangolo sacro, di Pitagora o di Plutarco - era usato, sin dall'epoca egizia, anche per tracciare facilmente angoli retti sul terreno, usando una corda con nodi posti a intervalli regolari. È anche l'unico triangolo rettangolo con i lati in proporzione aritmetica. Matila Ghyka riporta che tale triangolo, presso gli Achemenidi e i Sassanidi, costituiva la base per il tracciamento di cupole a sezione ovale, con rapporto tra gli assi 3/4 e rapporto tra i raggi 3/8 (cfr. Ghyka, The geometry of art and life, Sheed and Ward, New York 1946 [ristampa: Dover, New York 1977], p. 22).
16 Si potrebbe dedurre, dal taglio del terzo concio
allineato con la verticale dal centro della base
sull'ovale superiore e non su quello inferiore, che
Delorme abbia costruito prima l'ovale esterno e poi
quello interno. Una verifica, però, elimina
immediatamente questa possibilità: anzitutto i due ovali
non sarebbero più sovrapponibili ai grafici del
trattato, ma si perderebbero anche le relazioni
proporzionali; senza contare che è l'intradosso la parte
visibile della volta.
Dunque, prima è stato costruito l'ovale interno, poi
quello esterno - usando gli stessi centri - ed infine,
probabilmente per mantenere costanti i conci, la
verticale dal punto di mezzo è stata condotta sino
all'ovale esterno ad identificare l'inizio del taglio. In
tal modo il taglio non coincide con il punto d'unione tra
i due archi di cerchio: la piccola distanza, però, non
pregiudica la statica della volta.
17 Le due versioni del trait della trompe di Anet presentate da Delorme sono assolutamente concordanti tra loro per quanto concerne l'altezza della rampa, la pianta della trompe, l'ovale interno. Sono invece leggermente discordanti nei giunti tra quinto e sesto e tra sesto e settimo concio (nel trait del foglio 93 il quinto concio è più grande, mentre il sesto e settimo concio sono più piccoli); nella posizione del vertice A (di poco abbassato e spostato a destra nel trait del foglio 93, dove l'angolo al vertice è solo di poco superiore ai 90 gradi: 90.6°, mentre nel trait del foglio 96v. l'angolo è pari a 91.6°) e, sull'ovale esterno, nella posizione del punto di suddivisione tra terzo e quarto concio (l'ovale esterno del trait del foglio 93 è, in quel solo punto, rialzato rispetto all'altro di circa 1/15 dello spessore del concio). La sostanziale concordanza dei due grafici, in special modo dei due ovali, costituisce una prova ulteriore della loro intrinseca precisione, necessariamente dovuta all'applicazione di un metodo.
18 Anthony Blunt, Philibert De L'Orme, London 1958, p. 30. L'acquerello (Paris, Bibliothèque Nationale, Est Va 28), come nota Blunt, non ha iscrizioni; ma un altro disegno, della stessa mano e firmato Barbier, è datato 1698.
19 Il disegno presenta alcune incertezze
interpretative poiché mostra una mensola che sostiene il
lato orizzontale della volta: non è dunque chiara né
l'esatta lunghezza del lato né l'altezza della volta,
che potrebbe comprendere oppure no la mensola stessa.
L'unità di misura della scala grafica, presente al
centro del disegno, è la tesa:
1 tesa = 1.949 metri = 6 piedi; 1 piede = 0.325 metri =
12 pollici; 1 pollice = 0.02707 metri.
20 "Desquelles [i muri marcati G e H, della figura 2] si ie me fusse bien asseuré, & que ie les eusse faict faire, au lieu que la voûte de la trompe a de saillie, par le milieu de A à D, dix ou douze pieds, ie luy en eusse baillé vingt, ou vingt & quatre, & par le devant ie l'eusse faicte en forme ovale…". Delorme, cit., f. 90v.
21 Le misure sono indicate per eccesso. È anche da considerare, infatti, la possibile variazione dell'angolo al vertice della trompe, compreso tra 90° (valore ideale) e 91.6° (valore ricavato dal trait del foglio 96v.). Con l'aumentare dell'angolo aumenta anche l'altezza della volta.
22 Si è messo a punto un altro programma per computer (con passo di variazione di 1E-7 e limiti per la base CB compresi tra 5.7 e 8.3 piedi), in grado di verificare, per ciascuna scala, il numero di segmenti esattamente scomponibili in parti frazionarie; usando per le frazioni i primi 20 numeri naturali (figura 14). Solo il valore di 7.2 piedi permette di ottenere che tutti i segmenti indicati nella tabella 1 siano scomponibili in frazioni. Lo stesso si può ottenere per una lunghezza della base pari a 9.6 piedi: valore, però, troppo lontano dal limite massimo previsto e che produce un'altezza della volta di oltre 13.3 piedi.
23 La lunghezza del concio massimo è pari a 12.4 piedi, leggermente superiore ai 10/12 piedi citati da Delorme. È però da notare che quasi certamente la trompe prevedeva anche un trompillon impostato sul vertice, riducendo pertanto la lunghezza dei conci.
24 Delorme, cit., f. 132r. e f. 133r. Si vedano anche le note a pagina 39 dell'edizione anastatica curata da Pérouse de Montclos, cit.
25 Lo stesso Delorme (f. 106v.) si lamenta
della modesta qualità dei disegni del suo trattato,
addossandone la colpa agli incisori, usi - a suo dire -
persino a far bollire in acqua i fogli contenenti i suoi
disegni prima di incollarli sulle tavolette di legno.
Le variazioni, in ogni modo, sono comprese tra +/- 2% e
includono gli errori di costruzione, il ritiro della
carta prima dell'incisione e la deformazione delle pagine
dei volumi stampati.
|
|
Visitatori
dal 02/05/2000 |
