Gli inganni prospettici nelle rappresentazioni del vedutismo veneziano del Settecento

 Camillo Trevisan
trevisan@iuav.it

Articolo nel formato PDF (365 kB)

Data crezione: Agosto 1999

Osservando attentamente molti dipinti di Canaletto, Bellotto, Marieschi, Guardi o Carlevarijs, pur riconoscendo immediatamente i palazzi, i campielli, le chiese, i canali, le Scuole di Venezia, siamo spesso colpiti da una strana sensazione: non aver mai visto quegli edifici e quegli scorci della città.
O meglio, non averli mai visti in quel modo. In realtà li conosciamo bene, ma non li abbiamo mai osservati dal punto o con gli accorgimenti previsti dalla rappresentazione; sempre che, come spesso accade, gli edifici non abbiano subito delle ideali traslazioni o rotazioni rispetto alla loro reale posizione. Non abbiamo mai potuto abbracciare con lo sguardo centottanta gradi del bacino di San Marco¹, né osservare l'intera facciata delle Procuratie Nuove, contemporaneamente alla chiesa di San Marco e all'ala Napoleonica².
Questo breve saggio - di natura essenzialmente didattica - si occupa di queste rappresentazioni, con l'obiettivo di mettere in luce le loro caratteristiche peculiari, la loro genesi tecnica e i meccanismi di comprensione e di restituzione³.

Brevi cenni di prospettiva
Una prospettiva è il risultato dell'applicazione di un apparato di regole descrittive, costruite in modo tale che, opportunamente disposta la prospettiva rispetto ad un osservatore, tutti i punti ed i segmenti rappresentati nella prospettiva stessa si sovrappongono ai loro omologhi reali. Si deve poi aggiungere che l'osservatore deve guardare la rappresentazione con un solo occhio e immobile, poiché unico e fisso è il centro di proiezione della prospettiva (cfr. figura 1 A). In tal senso, e con queste restrizioni, la prospettiva è pertanto un succedaneo visivo della realtà.
Una fotografia - trascurando le distorsioni ottiche dell'obiettivo - è, a tutti gli effetti, una prospettiva nella quale il centro di proiezione è posto nel fuoco dell'obiettivo e la pellicola è il quadro prospettico. Questa osservazione sarà utile nella fase di comprensione, controllo e restituzione delle rappresentazioni, potendo verificare rapidamente e con esattezza molte ipotesi proprio per mezzo della fotografia. Nel farlo, non ci discosteremo poi molto dagli strumenti a quel tempo probabilmente usati per costruire quelle rappresentazioni⁴.
Tuttavia, in una prospettiva o in una fotografia - proprio per la necessità di essere a sua volta fruita visivamente da un osservatore - non sono verificate alcune caratteristiche ottiche, per noi del tutto evidenti e comuni. Ad esempio, noi percepiamo la grandezza degli oggetti osservati come funzione diretta dell'angolo visivo che li comprende: in una prospettiva la grandezza di un oggetto rappresentato è invece in proporzione inversa con la distanza dell'oggetto dal centro di proiezione e di vista (cfr. figura 1 D).
Ancora un esempio: disponendo una serie di cubi, tutti uguali tra loro, alla stessa distanza dal quadro prospettico, ci si attende di vedere rappresentati i cubi con le loro facce frontali sempre più piccole, man mano che queste si distanziano dal centro. Al contrario - e lo dimostra, a maggior ragione, l'applicazione del teorema di Talete - le rappresentazioni delle facce frontali mantengono invariata la grandezza: infatti, se, ad esempio, il quadro fosse appoggiato alle facce stesse, non vi sarebbe nessuno scorcio prospettico e tutte le facce rimarrebbero della loro grandezza reale. Inoltre, solo in un secondo momento - quando porremo l'occhio nel centro di proiezione - vedremo le facce più lontane dal centro anche più piccole, essendo più distanti dall'occhio di quelle centrali (cfr. figura 1 E).
Queste caratteristiche della prospettiva lineare prendono il nome di aberrazioni marginali e si manifestano quando l'occhio dell'osservatore non è posto nel centro di proiezione, unico punto che consente la corretta visione della prospettiva.
Queste apparenti anomalie costituiscono una delle basi più comuni degli inganni prospettici introdotti nelle rappresentazioni del vedutismo veneziano del Settecento.
È inoltre da tenere presente che, per comprendere la geometria degli oggetti rappresentati in una prospettiva e le loro mutue relazioni di posizione, è necessario formulare delle ipotesi sulla loro stessa geometria. In altre parole, la fruizione visiva e la comprensione di una rappresentazione prospettica è un'azione ricorsiva; nella quale, anche inconsapevolmente, l'osservatore identifica alcune forme geometriche elementari e alcune giaciture fondamentali (ad esempio, rettangoli o quadrati e segmenti certamente orizzontali o verticali), verifica la loro coerenza complessiva, corregge eventualmente alcuni presupposti e, su quella base, comprende la giacitura e la forma di altri oggetti rappresentati⁵.

Gli inganni prospettici
Oltre alle difficoltà appena accennate, la restituzione di una rappresentazione del vedutismo veneziano è ulteriormente complicata da alcuni espedienti applicati alle prospettive.
Questi potrebbero essere idealmente separati in due categorie: gli inganni lievi e quelli invece grevi.
Alla prima classe appartiene, ad esempio, la scelta di porre il punto di vista in posizione elevata⁶ oppure poco accessibile ed usuale⁷ (una finestra o un abbaino, un campanile, una barca, a Venezia molto comune per gli abitanti ma non per gli stranieri, principali destinatari dei dipinti); oppure l'uso del grandangolo, estendendo la cornice esterna della rappresentazione e dunque aumentando l'angolo di vista molto al di là della nostra capacità fisiologica⁸.
In tutti questi casi le aberrazioni marginali svolgono dunque un ruolo dominante, pur se non decisivo.
La rappresentazione sarà certamente osservata non dal corretto punto di vista o con il giusto angolo di campo e pertanto l'osservatore sarà parzialmente e temporaneamente ingannato: il ciclo della restituzione visiva, prima di convergere verso una realtà congruente, dovrà ripetersi più volte, richiedendo speciale attenzione e, dunque, quasi costringendo l'osservatore ad un'analisi approfondita ed estesa del dipinto.
Ben più raffinati e di assai più difficile comprensione sono invece i metodi che abbiamo classificato come pesanti; quasi sleali, se esistesse un galateo della prospettiva.
Il primo prevede la costruzione di una sorta di panoramica; essendo adottato, infatti, soprattutto nelle viste d'insieme, come, ad esempio, per il bacino di San Marco. Mantenendo fermo il punto di vista - spesso elevato di qualche metro rispetto al terreno o alla quota del mare - si eseguono due o più prospettive, del tutto normali, ruotando man mano la direzione principale di vista⁹. La rappresentazione finale sarà costruita dalla giustapposizione delle diverse prospettive, eseguendo dunque un ribaltamento dei quadri prospettici sul piano di rappresentazione (cfr. figura 2 A-D). In queste rappresentazioni, sono pertanto presenti più punti principali - uno per ciascuna prospettiva base - ma un solo punto di vista, con il vantaggio di poter rappresentare gruppi isolati e distanti di edifici tutti con vista quasi frontale.
Un altro metodo consiste nell'uso di più punti di vista - tipicamente due - ma di un unico piano di proiezione (cfr. figura 2 E-I). I due punti di vista, posti di norma alla stessa altezza, permettono di allargare virtualmente la scena - spesso un angusto campiello - senza introdurre forti aberrazioni marginali ai lati della rappresentazione¹⁰. Un geniale stratagemma, che costruisce una rappresentazione usando le parti migliori, le più descrittive e meno scorciate, di due diverse prospettive.
Ciascuno dei due ultimi metodi può essere a sua volta combinato con una o più d'una delle caratteristiche descritte all'inizio, costruendo in definitiva una rappresentazione unica, simile ma diversa alle tante altre di soggetto analogo.

Metodi di restituzione
Capire la struttura geometrica e volumetrica di una di queste rappresentazioni, ritrovarne i punti di vista o le giaciture dei quadri prospettici, oltre a soddisfare la nostra curiosità, è utile soprattutto per meglio comprendere la natura stessa della rappresentazione dell'architettura.
Oltre ai tradizionali e collaudati metodi di restituzione da singola prospettiva¹¹ - i quali permetteranno anche di rilevare eventuali anomalie proiettive -, nel nostro caso si rende disponibile un ulteriore, potentissimo strumento, reso possibile dal fatto che fortunatamente Venezia non è cambiata molto in questi ultimi secoli. Lo strumento è la città stessa. È la possibilità di verificare ed esperire personalmente le nostre teorie, anche per mezzo della fotografia e della cartografia storica o recente.
In questi casi, infatti, è utile non tanto restituire gli oggetti rappresentati - essendo disponibili gli originali - ma definire la posizione del punto di vista (o dei punti di vista) e le giaciture del quadro prospettico (o dei quadri prospettici), verificare se gli edifici rappresentati corrispondono o no agli edifici reali, se le loro posizioni relative concordano con la planimetria del sito. Stabilendo pertanto il luogo dove è stata costruita la rappresentazione, la sua configurazione geometrica ed eventuali manipolazioni proiettive.
Per semplicità, è utile suddividere il problema complessivo in segmenti di più facile soluzione.
È anzitutto utile trovare l'altezza dell'orizzonte: poiché tutte le rappresentazioni sono a quadro verticale, l'altezza dell'orizzonte corrisponderà anche all'altezza del punto di vista e viceversa.
Sarà sufficiente individuare una o più coppie di segmenti orizzontali - nella realtà ma non nella rappresentazione, come ad esempio la linea di gronda e l'attacco a terra di un edificio - e trovare i relativi punti di fuga nell'intersezione dei loro prolungamenti. Per quei punti passerà anche l'orizzonte (luogo dei punti di fuga degli infiniti fasci di rette orizzontali e non parallele al quadro). Per trovare la vera altezza del punto di vista, in metri, sarà sufficiente conoscere l'altezza di un edificio e applicare una proporzione (cfr. figura 3 A). Infatti, l'altezza totale dell'edificio, in metri, sta all'altezza misurata sulla rappresentazione, in centimetri, come l'altezza del punto di vista, in metri - valore da trovare - sta all'altezza dell'orizzonte, misurata sulla rappresentazione rispetto al piede dell'edificio. Questo calcolo prevede evidentemente che il suolo sia perfettamente orizzontale: condizione non molto lontana dalla verità, a Venezia.
Superato facilmente lo scoglio altimetrico (di norma, infatti, anche in presenza di più punti di vista, la loro altezza è la stessa), è ora necessario risolvere la planimetria. Si dovrà farlo senza conoscere in anticipo se la rappresentazione è una normale prospettiva o il frutto di un montaggio o di ribaltamenti.
Sarà pertanto inevitabile operare per accumulazione di indizi, interpretandoli poi e verificandoli anche in pratica. Le domande alle quali si dovrà dare risposta sono: quanti quadri prospettici sono stati usati? Quanti punti di vista? Qual è la loro giacitura e posizione? Gli edifici rappresentati mantengono la loro reale disposizione planimetrica?
In questo caso sarà di grandissima utilità una planimetria del sito (ad esempio la restituzione fotogrammetrica di Venezia, alla scala 1:500, contenente anche le quote di alcuni edifici).
Una prima indicazione si riferisce alla giacitura del piano di proiezione: supponendo, infatti, che nella realtà le linee di gronda e gli attacchi a terra degli edifici siano orizzontali, se è mantenuta l'orizzontalità anche nella rappresentazione, questo indica con certezza che il quadro prospettico è parallelo a quei segmenti. Nel caso si trovino quadri paralleli a facciate di edifici nella realtà non parallele tra loro, si dovrà necessariamente concludere che quella rappresentazione è una panoramica oppure che gli edifici hanno subito una rotazione.
Un'altra utile indicazione viene dagli allineamenti di punti riferiti a edifici diversi: supponendo, infatti, che un edificio nasconda parzialmente un'altra costruzione, si potranno individuare, nella pianta, il punto che indica lo spigolo dell'edificio più vicino al punto di vista e il punto, sulla facciata dell'altro edificio, dove lo spigolo si proietta (cfr. figura 3 G). Tracciando una retta per i due punti, avremo la certezza che il punto di vista si trova lungo quella retta (o, almeno, che il punto di vista riferito a quel gruppo di edifici si trova lungo quella retta). Per identificare la posizione esatta, si potrà procedere in vari modi: definendo due o più rette (il punto di vista si troverà nel loro punto di intersezione, ammesso che sia unico), oppure operando per proporzione, conoscendo le altezze degli edifici in esame (cfr. figura 3 C-G). Anche in questo caso, se si identificano con certezza più punti di vista - ben separati tra loro - si dovrà dedurre che la rappresentazione è formata da un montaggio di più prospettive.
Un ulteriore parametro di indagine è dato dall'analisi geometrica delle ombre proprie e portate dagli edifici che compongono la scena. Spesso potranno dirimere lo spinoso dubbio: la rappresentazione è ottenuta da un ideale spostamento degli edifici ovvero da un cambiamento del punto di vista o del quadro?
Per concludere, è utile ricordare l'assoluta necessità di una verifica incrociata delle ipotesi fatte.
Tale verifica dovrà pertanto essere attuata operando per saturazione; con metodi diversi e, possibilmente, usando diversi parametri e, sempre, con sovrabbondanza di controlli.
Infatti, non solo le rappresentazioni sono - o possono essere - intrinsecamente poco precise (e in special modo le loro riproduzioni a stampa), ma soprattutto è del tutto normale l'introduzione di lievi modifiche topografiche e accomodamenti proiettivi, ad esempio attorno alle linee di giuntura tra i piani prospettici, oppure per ragioni compositive, pittoriche.
Solo se le ipotesi fatte risultano tutte congruenti e connesse, riscontrate da molti indizi - ben distribuiti su tutta la rappresentazione - e possibilmente verificate anche per mezzo di fotografie, si potrà concludere positivamente la ricerca.
L'analisi geometrica e la comprensione di una rappresentazione del vedutismo veneziano del Settecento non è dunque un puro, quasi monotono, esercizio tecnico; dove il problema consiste nel cercare la soluzione, forse complessa ma certamente esistente. Piuttosto, nel suo procedere, è per certi versi simile allo studio di una rappresentazione preprospettica, nella quale nulla o quasi è evidente e ciascun passaggio deve essere provato e consistente: ogni veduta, infatti, è unica e caratterizzata da elementi singolari, combinati in modo sempre variato e spesso imprevedibile.
Nel nostro caso, tuttavia, gli edifici rappresentati sono tuttora esistenti e sappiamo per certo che l'immagine può essere scomposta in nuclei prospettici, isolati oppure coordinati proiettivamente, ma sempre rispondenti alle leggi fondamentali della prospettiva e legati tra loro dalle mutue relazioni instaurate dai tre enti considerati: la disposizione planimetrica degli edifici reali, la posizione dei punti di vista e la giacitura dei quadri prospettici.

NOTE

1) Canaletto, Il bacino di San Marco verso Est, Boston, Museum of Fine Arts (Puppi, n. 161 A).

2) Canaletto, Piazza San Marco, verso la Libreria, tra gli scorci della Basilica e della chiesa di San Geminiano, Hamstead Marshall (Berkshire), coll. Craven (Puppi, n. 133 A). La veduta comprende un angolo orizzontale di oltre 140 gradi.

3) Per una estesa analisi dei dipinti e approfondimenti sui metodi prospettici dei vedutisti, si veda anzitutto: Lionello Puppi, L'opera completa del Canaletto, Rizzoli, Milano 1968 (per il Canaletto, i riferimenti delle note sono a questo testo); William George Constable, Canaletto: Giovanni Antonio Canal, 1697-1768, Clarendon Press, Oxford 1962; André Corboz, Canaletto, una Venezia immaginaria, Alfieri Electa, 1985 (in particolare i saggi: Prova della verità topografica, Camera obscura, oscura o ottica, Prospettiva canalettiana); André Corboz, Sur la prétendue objectivité de Canaletto, Arte veneta XXVIII (1974), pp. 205-18; Maria Agnese Chiari, Nuove osservazioni su Canaletto e la camera ottica, Arte veneta XXXVIII (1984), pp. 106-18; Ettore Camesasca, L'opera completa del Bellotto, Rizzoli, Milano 1974 (per il Bellotto, i riferimenti delle note sono a questo testo); Stefan Kozakiewicz, Bernardo Bellotto, Gorlich, Milano 1972; Luigina Rossi Bortolatto, L'opera completa di Francesco Guardi, Rizzoli, Milano 1974 (per il Guardi, i riferimenti delle note sono a questo testo); Aldo Rizzi, Luca Carlevarijs, Alfieri, Venezia 1967; Ralph Toledano, Michele Marieschi: l'opera completa, Mondadori, Milano 1988; Bernard Aikema, Boudwijn Bakker, Painters of Venice: the story of the venetian "veduta", Amsterdam, Swartz 1990 (catalogo della mostra tenuta ad Amsterdam nel 1990-91); Pietro Zampetti, I vedutisti veneziani del Settecento, Alfieri, Venezia 1967 (catalogo della mostra del 1967 a Palazzo Ducale, Venezia); Isabella Reale, Dario Succi, Luca Carlevarijs e la veduta veneziana del Settecento, Electa, Milano 1994; Isabella Reale, Luca Carlevarijs: le fabriche, e vedute di Venetia (Venezia 1703), Marsilio, Venezia 1995 (catalogo della mostra tenuta a Udine nel 1995-96).

4) Al museo Correr di Venezia è conservata una camera ottica con iscrizione "A. Canal". Strumenti simili a quello sembra fossero abitualmente usati per la costruzione degli schizzi preparatori: al riguardo, oltre ai saggi indicati nella nota precedente, si veda anche Martin Kemp, La scienza dell'arte, Giunti, Firenze 1994.

5) Al riguardo si veda l'articolo: Programma Euclid: restituzione prospettica funzione di regole compositive; presso il sito Internet http://www.iuav.it/dpa/ricerche/trevisan/euclid2.htm (euclid.pdf).

6) Ad esempio: Canaletto, Il Canal Grande da campo San Vio, presso il ponte di Rialto, Milano, coll. Crespi (Puppi, n. 13).

7) Ad esempio: Canaletto, Ricevimento dell'ambasciatore francese a Palazzo Ducale, Leningrado, Ermitage (Puppi, n. 31); Canaletto, La punta della Dogana, Vienna, Kunsthistorisches Museum (Puppi, n. 38).

8) Ad esempio: Francesco Guardi, Il doge nella Sala del Maggior Consiglio, ringrazia i patrizi per la sua elezione, Nantes, Musée des Beaux-Arts (Rossi Bortolatto, n. 448); Bernardo Bellotto (attribuito), Piazza San Marco, dalla torre dell'Orologio verso le Procuratie Nuove, Lille, Musée des Beaux-Arts (Camesasca, n. 289 A, si veda anche la nota 2, per una equivalente veduta del Canaletto); Canaletto, La Piazzetta, con la Libreria, verso Ovest, Alton (Hampshire), coll. Hampden (Puppi, n. 111).

9) Ad esempio, oltre al già citato Bacino di San Marco di Boston: Canaletto (da alcuni attribuito a Michele Marieschi), La chiesa della Salute, Parigi, Louvre (Puppi, n. 23 B); Francesco Guardi (da Constable attribuito a Marieschi), Canal Grande a San Geremia, Baltimore, Museum of Art (Rossi Bortolatto, n. 104); Canaletto, Piazza San Marco, con gli scorci della Basilica e del lato Nord-Est, Hartford, Wadsworth Atheneum (Puppi, n. 190 A).

10) Ad esempio: Canaletto, La Piazzetta verso Sud, Roma, Galleria Nazionale (Puppi, n. 139 A); Canaletto, Il Bucintoro di ritorno al Molo il giorno dell'Ascensione, Inghilterra, coll. privata (Puppi, n. 67 C); Canaletto, La Piazzetta verso Nord, Woburn Abbey, coll. duca di Bedford (Puppi, 86 A).

11) Per una più approfondita e completa disamina del problema, si rimanda, ad esempio, a L'impiego della fotografia nel rilievo, in AA.VV., Teorie e metodi del disegno, CittàStudi, Milano, 1994.

FIGURE

Figura 1. Costruzione e alcune caratteristiche fondamentali della prospettiva

Il grafico A illustra il metodo più semplice e diretto per la costruzione di una prospettiva a quadro verticale. Da esso, tra l'altro, si ricavano i seguenti concetti: segmenti reali appartenenti al quadro non sono scorciati in prospettiva; segmenti paralleli al quadro mantengono la loro giacitura nella proiezione; segmenti tra loro paralleli nella realtà concorrono in prospettiva verso un unico punto di fuga, uno per ciascuna direzione nello spazio, esclusi i fasci di rette parallele al quadro; il punto di fuga di una retta (o meglio di un fascio di rette parallele e, pertanto, di una direzione) è dato dalla traccia sul quadro della retta parallela alla direzione data e passante per il centro di proiezione: così, ad esempio, il punto di fuga del fascio di rette orizzontali, parallele ad una diagonale del quadrato (per C₁E₁, nella pianta) è dato dal punto PD (punto di distanza, poiché la distanza tra PD e PP1₁ è congruente alla distanza tra quest'ultimo e PV₁), traccia sul quadro della retta per PD e per PV₁ e parallela alla retta per C₁E₁; seguendo quanto appena detto, il punto principale (proiezione del punto di vista, eseguita perpendicolarmente al quadro) è anche il punto di fuga (in prospettiva) di tutte le rette perpendicolari al quadro (parallele, dunque, alla retta per PV e PP); l'orizzonte è il luogo dei punti di fuga degli infiniti fasci di rette orizzontali e non parallele al quadro: poiché il punto principale è il punto di fuga di un fascio di rette orizzontali, ne segue che, definito il PP o qualsiasi altro punto di fuga di un fascio di rette orizzontali, è definito anche l'orizzonte (e, dunque, l'altezza del punto di vista).

Grafico B. È noto che osservando una fotografia di un oggetto (o una prospettiva, poiché è lo stesso) non è generalmente possibile stabilire in modo univoco la forma di quest'ultimo: ad esempio un tronco di piramide può senz’altro costruire un'immagine prospettica identica a quella di un parallelepipedo. Vale a dire che nel passaggio dalle tre dimensioni dello spazio reale alle due dimensioni della prospettiva piana, vanno inevitabilmente perdute alcune informazioni metriche e morfologiche. Ogni oggetto, fissato il centro di proiezione (PV) ed il piano di proiezione prospettica (quadro), fornisce un’unica immagine su questo ma, viceversa, fissato ancora il PV, il quadro e l’immagine prospettica, esistono infinite configurazioni tridimensionali alle quali questa può riferirsi. Tra queste potremo scegliere quella corretta solo possedendo alcune informazioni supplementari, che ci permettano di eliminare tutte le configurazioni errate mantenendo l’unica che verifica tutte le condizioni (sempre che una soluzione esista e sia unica). Nel nostro caso le ulteriori informazioni sono date dagli stessi edifici reali. Se, ad esempio, si è certi di possedere un'immagine di un cubo si potrà, di norma, collocarlo correttamente nello spazio: infatti, i parametri impiegati nella restituzione prospettica sono i medesimi utilizzati per la costruzione della stessa prospettiva, con l’ovvia differenza che mentre in quest’ultima i parametri sono liberi e determinano la resa prospettica, al contrario nella restituzione costituiscono le incognite da ricercare.

Il grafico C illustra la proporzione esistente tra i segmenti reali proiettati su piani diversi, tra loro paralleli. Questo comporta che, traslando il quadro parallelamente a se stesso (escludendo il caso del quadro contenente il punto di vista), l'immagine prospettica non cambia, a meno di un fattore di scala: non vengono però modificati i rapporti tra i segmenti proiettati, né l'angolo che essi formano tra loro sul quadro. In una fotografia, dunque, mantenendo fisso il centro ottico dell'obiettivo e la direzione di ripresa, la prospettiva non è affatto modificata dal variare dell'obiettivo, sia esso un grandangolo o un teleobiettivo: cambia esclusivamente la porzione di spazio proiettato sul fotogramma.

Il grafico D dimostra, invece, che lo scorciamento prospettico è in funzione inversa della distanza dell'oggetto dal PV. I segmenti AB e CD sono infatti uguali tra loro. Poiché la distanza E-PV è la metà di F-PV, ne segue che C'D' è la metà di A'B', per qualunque posizione del quadro (vedi grafico C).

Infine, il grafico E illustra un'altra caratteristica della prospettiva lineare. Gli oggetti (cubi tutti uguali tra loro) sono disposti alla stessa distanza dal quadro. La prospettiva mostra le loro facce frontali tutte uguali tra loro, anche per i cubi più distanti dal PV. Osservando la prospettiva dal giusto punto (posto sopra il punto principale, con distanza PP-PV), le facce più esterne saranno anche più lontane dall'occhio dell'osservatore e, dunque, saranno viste più piccole. Nel grafico, la retta per il punto principale rappresenta il quadro verticale, visto in pianta, se si considera la configurazione proiettiva; rappresenta invece l'orizzonte se si prende in esame la prospettiva, ruotata idealmente di 90° per disporla orizzontalmente. Nella fase di comprensione, ricostruzione spaziale e restituzione prospettica è infatti molto utile sovrapporre la pianta degli oggetti rappresentati e il ribaltamento in pianta della prospettiva o della rappresentazione definita dalla configurazione proiettiva.

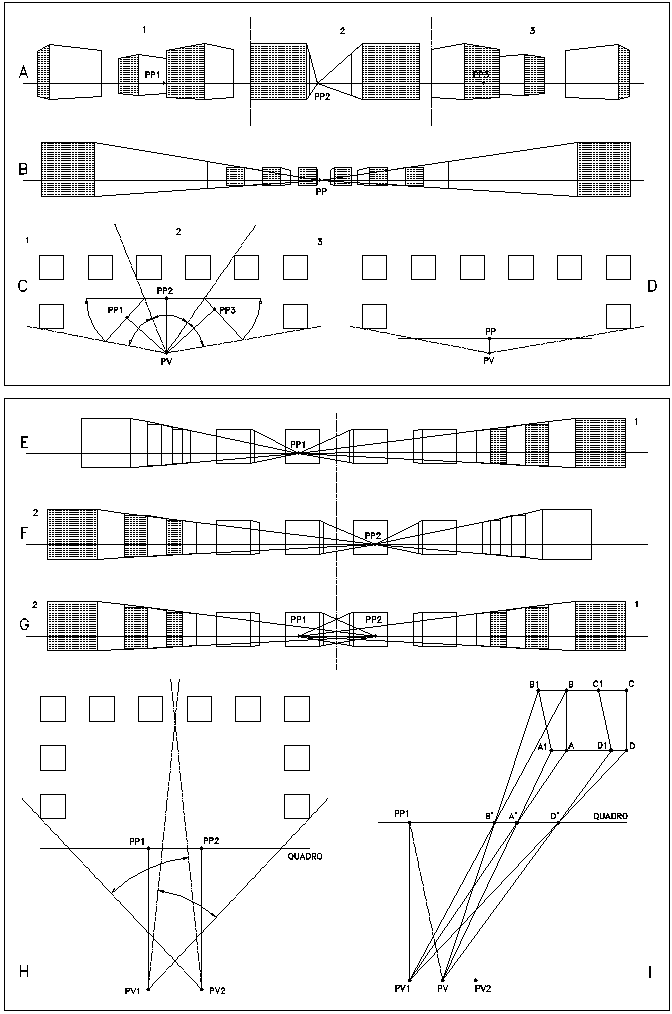
Figura 2. Schemi proiettivi degli inganni prospettici usati dai vedutisti veneziani del Settecento

In questi grafici sono stati sintetizzati i due metodi indicati nel testo per alterare la prospettiva piana: la panoramica, ovvero il ribaltamento su di un unico piano di più quadri prospettici tra loro inclinati (in alto), e l'uso di due punti di vista (in basso).
Per quanto riguarda il primo metodo, il grafico A mostra il risultato finale del ribaltamento, indicato nel grafico C, il quale riproduce la pianta degli oggetti rappresentati (alcuni cubi, uniformemente distribuiti sul piano orizzontale), le giaciture dei tre quadri prospettici verticali e i loro ribaltamenti sul piano finale di rappresentazione. Come si può notare, non è necessario che i punti principali cadano al centro delle porzioni di quadro di ogni singola prospettiva: è invece utile che le unioni tra le varie rappresentazioni cadano in punti morti, e in ogni caso non all’interno delle facciate degli edifici rappresentati. La facciata, infatti, risulterebbe spezzata, poiché le due metà convergerebbero verso punti di fuga diversi tra loro.
In questo caso il punto di vista è unico ma esistono più punti principali, uno per ciascun quadro prospettico: dunque, alcuni segmenti reali, pur perpendicolari al piano della rappresentazione finale, non concorrono verso il punto principale PP₂.

Il grafico B illustra invece il risultato di una normale prospettiva piana (per lo schema di pianta, si veda il grafico D). Come si può notare, l'ampio angolo di campo (circa 160°) introduce delle fortissime aberrazioni marginali. Tuttavia, in questo caso, come era giusto attendersi, tutti i segmenti perpendicolari al quadro concorrono verso l'unico punto principale PP.
Il confronto tra i grafici A e B mette in luce un'altra interessante caratteristica: le due rappresentazioni, pur molto diverse tra loro nella morfologia degli oggetti proiettati, contengono non solo gli stessi oggetti ma anche le stesse parti degli oggetti. In altre parole, poiché il punto di vista è unico, fisso e comune ad entrambe le rappresentazioni, l'osservatore - comunque sia disposto il quadro o la direzione principale di vista - vedrà sempre la medesima scena, sia pur proiettata in modo diverso, secondo l'inclinazione del quadro stesso.
Il secondo metodo prevede invece l'uso di più punti di vista (tipicamente due) e la successiva giustapposizione di alcune parti delle prospettive prodotte, per costruire la rappresentazione definitiva. In questo caso la rappresentazione finale (grafico G) è ottenuta dalla somma della parte destra del grafico E, e dalla parte sinistra del grafico F.
Il grafico H mostra la pianta della scena rappresentata, la giacitura del quadro prospettico e la posizione dei due punti di vista PV₁ e PV₂ e dei due punti principali.
Da notare che le due parti del grafico G, proprio per la loro diversa natura e genesi proiettiva, possono essere traslate orizzontalmente, allontanandole o avvicinandole tra loro, per aumentare o diminuire l'effetto di ideale allargamento dello spazio rappresentato: un’attenta analisi geometrica dello spazio intermedio potrà dunque essere di grandissimo aiuto nella fase di restituzione.
L'esistenza di più di un punto di vista comporta necessariamente la presenza di altrettanti punti principali: nel grafico G, infatti, tutti i segmenti ortogonali all'unico quadro dovrebbero convergere verso un unico punto di fuga, il punto principale. In realtà i segmenti ortogonali al quadro di ciascun lato della rappresentazione concorrono verso un loro punto principale. Pertanto, mantenendo costante la scena reale, non esiste la possibilità di riprodurre la stessa rappresentazione per mezzo di un unico punto di vista, ma è necessario modificare la geometria degli oggetti reali.
Il grafico I illustra appunto questa deformazione. Il quadrato ABCD, proiettato dal punto PV₁, si sovrappone, nel quadro, alla proiezione del parallelogramma A₁B₁C₁D₁, dal punto PV. Le due figure, osservate dai rispettivi punti di vista, sono pertanto equivalenti e dunque il grafico G può essere ottenuto deformando opportunamente gli oggetti reali e osservandoli poi dal punto di vista adottato per la loro deformazione.
L'inclinazione del segmento A₁B₁ deriva da quella del segmento PV PP₁: infatti, poiché il segmento A₁B₁ deve concorrere - nella prospettiva - in PP₁, è necessario che - nella realtà - i due segmenti (PV PP₁ e A₁B₁) siano paralleli tra loro (come si è visto, il punto di fuga di una direzione è dato dalla traccia sul quadro della retta parallela alla direzione data e passante per il punto di vista).
Evidentemente, il quadrilatero A₁B₁C₁D₁ potrebbe assumere infinite altre giaciture e dimensioni: quelle scelte lo rendono però più vicino al quadrato reale ABCD.

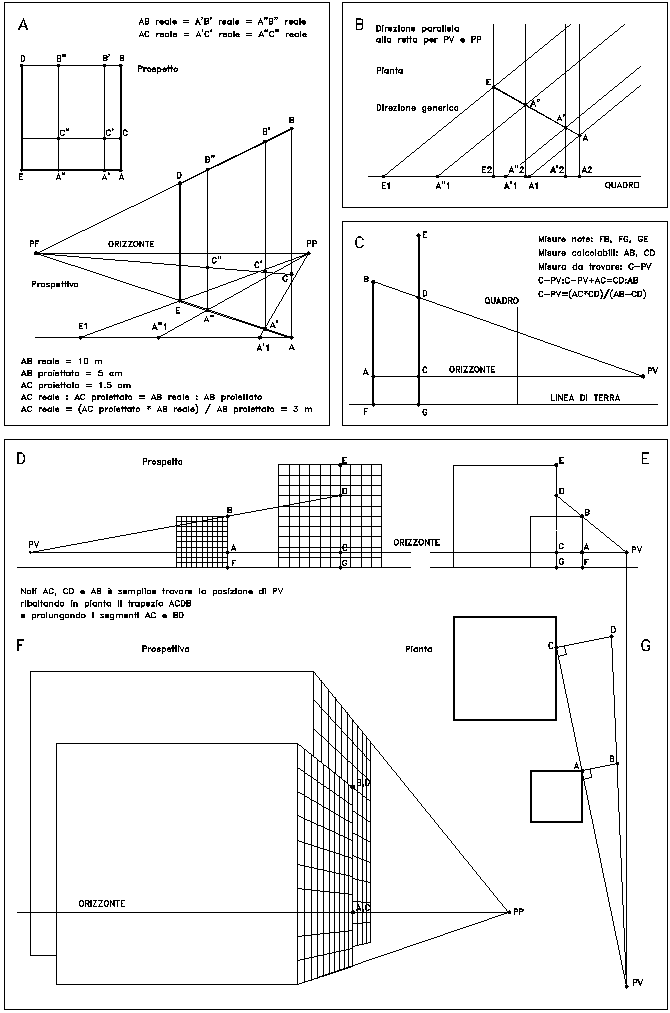
Figura 3. Schemi per il reperimento delle coordinate del punto di vista

Grafico A. Determinazione dell'altezza di un generico punto, posto sulla facciata di un edificio, essendo nota l'altezza dell'edificio stesso. Il trapezio ABCD rappresenta la prospettiva di un rettangolo reale (ad esempio, la facciata di un edificio), avente i segmenti AD e BE orizzontali e AB e ED verticali e inclinazione generica - ed anche sconosciuta - rispetto al quadro. Dunque, tracciata una retta qualsiasi - che passi per PF, punto di fuga di BE e AD -, ad esempio C PF, questa suddivide il segmento AB in due parti aventi tra loro un dato rapporto, variabile con il variare della retta C PF.

Lo stesso rapporto, tuttavia, si instaura tra tutti i segmenti generati da segmenti paralleli ad AB (nella realtà, infatti, le rette C PF, A PF e B PF sono parallele tra loro). Così, AC/CB=A'C'/C'B'=A"C"/C"B", e così via. D'altra parte, la retta nella realtà è senz'altro orizzontale e parallela ad AD e a BE. Dunque, nella realtà, i segmenti AC, A'C' e A"C" sono uguali tra loro. Pertanto, per conoscere, ad esempio, l'altezza del punto C', nota l'altezza dell'intero edificio e il punto di fuga delle orizzontali, è sufficiente tracciare una verticale per C' ed eseguire una semplice proporzione: AC reale = (AC proiettato * AB reale) / AB proiettato.
Lo stesso metodo può essere adottato per reperire l'altezza dell'orizzonte e dunque del punto di vista.
Inoltre, le rette dal punto principale per A', A", E, definiscono, sulla retta orizzontale per A, i punti A'₁, A"₁, E₁. Questi rappresentano le proiezioni ortogonali sul quadro dei punti A', A", E: infatti, le rette che nella prospettiva convergono verso il punto principale, nella realtà sono tutte parallele tra loro e ortogonali al quadro. Per la proiezione dei punti sul quadro, è anche possibile scegliere un qualunque punto posto sull'orizzonte (luogo dei punti di fuga dei fasci di rette orizzontali), escluso PF.
In questo caso si tratterà ancora di una proiezione sul quadro, compiuta da un generico fascio di rette orizzontali e parallele tra loro, con angolo sconosciuto rispetto al quadro: saranno però mantenute le mutue proporzioni tra i veri segmenti AA', A'A" e A"E (per il teorema di Talete, grafico B).
Grafico C. Definizione della posizione del punto di vista, nota la retta alla quale appartiene il punto stesso, la lunghezza di due segmenti - orizzontali o verticali - sovrapposti nella proiezione ma non nella realtà e la loro distanza in pianta. Conoscendo la lunghezza del segmento FB (altezza del primo edificio), è semplice trovare la lunghezza AB, per proporzione, come già descritto nel punto precedente (vedi grafico A). La lunghezza CD si trova anch'essa per proporzione, nota l'altezza GE del secondo edificio. Nota la distanza AC (uguale ad FG; la retta per A e per C contiene anche il punto di vista), è possibile definire la distanza C PV con una semplice proporzione, usando le proprietà dei triangoli simili A-B-PV e C-D-PV.
Pertanto: C PV = (AC * CD)/(AB - CD).
Grafici E-G. È qui meglio descritto - in pianta, prospetti e prospettiva - il metodo già visto nel grafico precedente (invertendo la posizione dei segmenti verticali rispetto al PV). I punti B e D, appartenenti ad edifici diversi, sono sovrapposti in prospettiva. Questo indica che i due punti sono allineati con il punto di vista. Conoscendo l'altezza di B rispetto ad A (con il punto A posto alla stessa altezza del PV), l'altezza di D rispetto a C e la distanza tra A e C (misurabile su di una pianta della città), si imposta la retta per A e C. Il punto di vista deve appartenere a questa retta.
È pertanto necessario trovare la distanza di PV da A. Ribaltando in pianta le altezze CD e AB si definisce un trapezio (ABDC). Prolungando i segmenti CA e DB si identifica il punto di vista.
La prima parte del metodo - l'identificazione di due punti sovrapposti in prospettiva, riconoscibili e reperibili nella pianta del sito - può essere usata anche senza la conoscenza delle altezze. Infatti identificando due o più rette (simili a CA), il punto di vista si trova nel loro punto di intersezione, dovendo appartenere a tutte le rette.
Nel caso si trovino due o più punti di intersezione, ben distanziati tra loro, molto probabilmente la rappresentazione complessiva è frutto dell'unione di due o più prospettive, ciascuna eseguita da un punto diverso (cfr. figura 2 G). Se, al contrario, si identifica un solo punto di vista ma più punti principali (più facciate non parallele tra loro nella realtà ma con i loro segmenti orizzontali che rimangono tali nella prospettiva), si tratterà invece di un montaggio di varie prospettive ribaltate sul piano della rappresentazione (cfr. figura 2 A). Queste ipotesi, evidentemente, valgono solo se non sono state modificate le reali posizioni planimetriche degli edifici rappresentati.