Erwin Panofsky
nel suo saggio del 1927 Die Perspektive als "symbolische Form", propone
un metodo di rappresentazione secondo la prospettiva angolare degli Antichi.
Nel descriverlo, prendendo fondamento da Vitruvio (“Item
scaenographia est frontis et laterum abscedentium adumbratio ad circinique
centrum omnium linearum responsus”, Vitruvio, De Architectura,
1, 2, 2) il Panofsky scrive: "Ora,
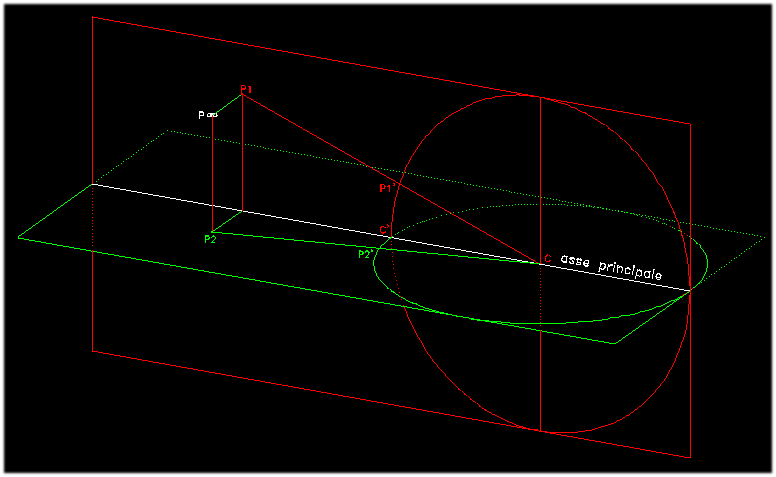
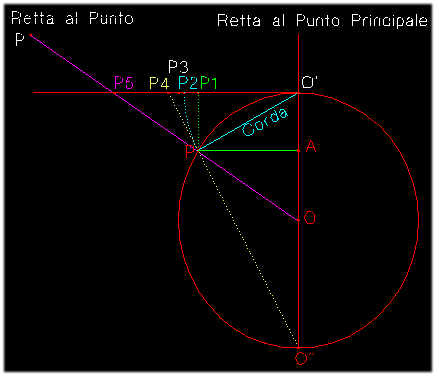
se si esegue la costruzione con l'aiuto di un simile cerchio di proiezione
(ove, come abbiamo detto, gli archi di cerchio siano sostituiti dalle corde
sottese) si giunge al risultato che coincide in un punto essenziale con i
dipinti conservati: i prolungamenti delle linee di profondità non
concorrono, con una convergenza rigorosa, in un punto; essi si incontrano
(poiché svolgendo il cerchio, i suoi settori divergono in una qualche
misura al vertice), convergendo soltanto debolmente a due a due in più
punti, i quali giacciono tutti su un asse comune, tanto che ne nasce
l'impressione di una lisca di pesce".
[E. Panofsky, Die Perspektive
als "symbolische Form", in Vorträge der
Bibliothek Warburg, Teubner,
Leipizig-Berlin 1927 (ed. it. La prospettiva come "forma simbolica" e
altri scritti, Feltrinelli, Milano 1961 [succ. 1966, 1980]), p. 44].
Per una disamina complessiva del metodo, si veda anche:
- Decio Gioseffi, Perspectiva artificialis - per la storia della
prospettiva - spigolature e appunti, Università degli Studi di
Trieste, Trieste 1957.
- Richard Tobin, Ancient perspective and Euclid's Optics, in
"Journal of the Warburg and Courtauld Institutes", Warburg Institute and
University of London, vol. 53 (1990), pp. 14-41 e figure.
- Francesca Incardona, Euclide - Ottica - Immagini di una teoria
della visione, Di Renzo Editore, Roma 1996.
- a cura di Pierre Gros, traduzione in italiano, con note e
commenti e testo latino a fronte, di: Vitruvio - De
Architectura, Einaudi, Torino 1997. Nella
pagina Internet http://www.iuav.it/dpa/ricerche/trevisan/panofsky/panofsky.htm
è disponibile un programma freeware per la generazione di
rappresentazioni eseguite seguendo il metodo proposto dal Panofsky. |
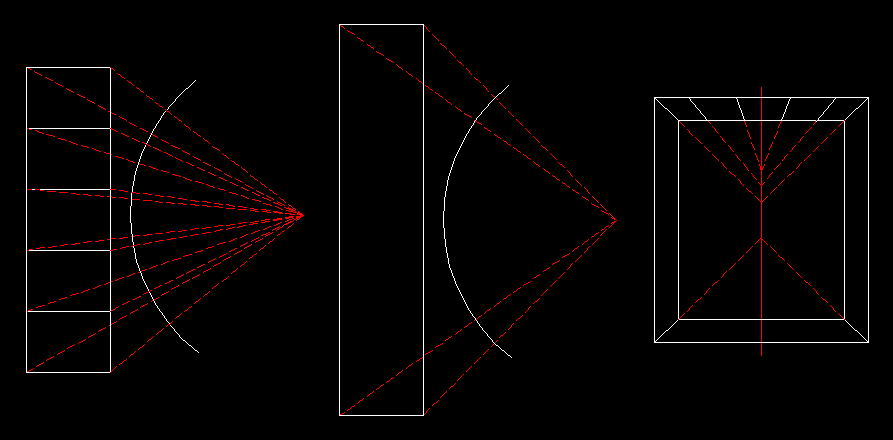
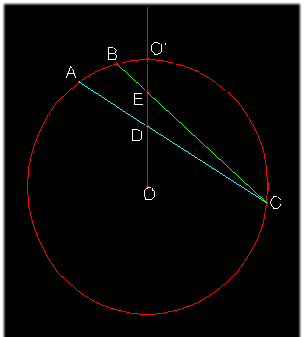
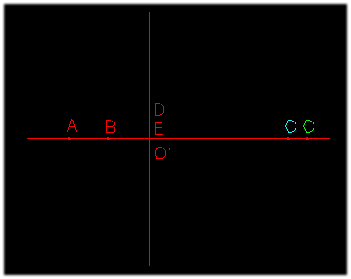
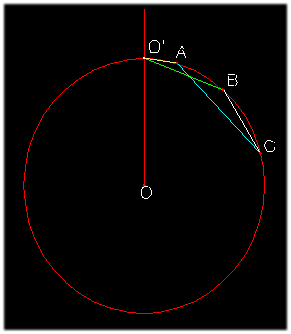
Costruzione
di una scatola spaziale secondo la prospettiva angolare
degli Antichi proposta dal Panofsky (E. Panofsky, La prospettiva...,
op. cit., p. 46, fig. 5). Da questa immagine si può dedurre che il
Panofsky considera la proiezione come ortografica.
A sinistra la pianta, al centro l'alzato e a destra l'immagine prospettica
ottenuta mediante la combinazione dei segmenti determinati sul "cerchio di
proiezione". |