Nell'ambito dello studio degli encausti pompeiani e della loro restituzione prospettica si sono analizzati vari tipi di proiezione degli oggetti, allo scopo di evidenziarne le caratteristiche particolari e compararle sinotticamente. L'oggetto utilizzato per le prove è un cubo, di lato pari a 9 unità, i cui segmenti sono stati però divisi in un gran numero di parti allo scopo di verificare sia la messa in prospettiva veloce dei soli estremi di ogni segmento, sia la sua costruzione rigorosa sottoponendo a trasformazione prospettica ogni punto ad esso appartenente. Le facce del cubo sono state a loro volta suddivise con linee equidistanti, mentre la disposizione del cubo è con le facce parallele al sistema cartesiano. Le prove effettuate riguardano vari casi.

PROSPETTIVA A QUADRO VERTICALE. Costituisce la rappresentazione di riferimento per tutte le altre proiezioni ed è anche usata per la verifica delle ipotesi espresse da Decio Gioseffi [D. Gioseffi, Perspectiva artificialis, Quaderno N° 7 dell'Istituto di Storia dell'Arte Antica e Moderna, Trieste 1957]. Nei grafici vengono anche rappresentate, in giallo, le rette che concorrono al Punto Principale a partire dai quattro spigoli del cubo perpendicolari al Quadro e paralleli alla direzione di vista.

PROSPETTIVA A PIANO INCLINATO CON ORTOPROIEZIONE SUL QUADRO VERTICALE. Il punto reperito sul piano inclinato viene successivamente proiettato perpendicolarmente sul quadro verticale utilizzando un "punto all'infinito" (ortoproiezione). In questa proiezione le linee verticali si inclinano verso l'interno (verso l'esterno se il piano viene ruotato dalla parte opposta), e risultano tanto più inclinate quanto più viene ruotato il piano. Le rette perpendicolari al quadro convergono sempre verso un unico punto di concorso.

PROSPETTIVA A PIANO INCLINATO CON ROTAZIONE SUL QUADRO VERTICALE. Il punto di intersezione tra la retta che unisce il PV e il punto da mettere in prospettiva con il piano inclinato, viene successivamente ribaltato sul quadro verticale usando come asse di rotazione la retta di intersezione tra i due piani. Viene pertanto riportata sul quadro non l'altezza del punto sul piano inclinato (un cateto del triangolo rettangolo), ma la sua distanza dall'asse di rotazione (l'ipotenusa dello stesso triangolo). Come per il caso precedente le linee verticali si inclinano verso l'interno, ma in modo meno marcato. Anche in questo caso le rette perpendicolari al quadro convergono verso un unico punto.

PROSPETTIVA SFERICA CON ORTOPROIEZIONE. Il punto di intersezione tra retta P-PV (centro della sfera) e sfera viene riportato sul quadro perpendicolarmente rispetto al quadro stesso: viene perciò riportata l'altezza del punto nella coordinata Y della prospettiva e la sua posizione planimetrica diviene la coordinata X della prospettiva. Come si può notare le rette perpendicolari al Quadro rimangono rettilinee, mentre i segmenti paralleli al quadro subiscono una deformazione sferica (in rosso sono evidenziati i segmenti "ideali" che identificano i lati del cubo: non sono stati dunque ottenuti dalla proiezione ma servono solamente per una valutazione visiva della deformazione dei segmenti nella proiezione. Nei grafici a sinistra, i cerchi azzurri indicano la posizione del punto sulla sfera).

PROSPETTIVA SFERICA STEREOGRAFICA. I punti vengono contro-proiettati da un polo che sta sul cerchio massimo della sfera, opposto al quadro. In questo caso le coordinate dei punti sulla sfera vengono modificate dalla contro-proiezione sul quadro.  Anche in questo caso, però, le rette perpendicolari al quadro rimangono rettilinee nella proiezione. Da notare che, come anche nel caso precedente ed in tutti gli altri, il PP si mantiene evidentemente unico.

PROSPETTIVA CILINDRICA A CILINDRO VERTICALE CON ORTOPROIEZIONE. Scelto un centro di proiezione posto sull'asse verticale del cilindro, si contro-proiettano, ortogonalmente al quadro, i punti intercettati dai raggi proiettanti sulla superficie del cilindro. Evidentemente i segmenti verticali rimangono rettilinei (dato che il cilindro è verticale), mentre quelli orizzontali e paralleli al Quadro si deformano in modo simile alle proiezioni sferiche.

PROSPETTIVA A CILINDRO VERTICALE A BASE ELLITTICA CON ORTOPROIEZIONE. In questo caso, simile a quello precedente, il cilindro non è a base circolare ma ellittica. Se l'ellisse presenta il suo semiasse minore perpendicolare al quadro la proiezione risulta "allargata" rispetto alla precedente. Viceversa se è l'asse maggiore ad essere perpendicolare al quadro la proiezione apparirà "allungata" sull'asse verticale.

PROSPETTIVA ELLISSOIDICA CON ORTOPROIEZIONE. Questo metodo proiettivo è simile a quello presentato nel caso del cilindro con ortoproiezione, con l'unica differenza data dall'uso, anziché di una sfera, di un ellissoide. In questo caso l'asse orizzontale minore dell'ellissoide è perpendicolare al quadro.

PROSPETTIVA ELLISSOIDICA CON ROTAZIONE DELL'ELLISSE GENERATRICE DI 90 GRADI. La proiezione è simile alla precedente ma è l'asse orizzontale maggiore dell'ellissoide ad essere perpendicolare al quadro.

PROSPETTIVA A DOPPIO CILINDRO PROPOSTA DAL PANOFSKY . In questo tipo di proiezione vengono usati due cilindri a base circolare: uno orizzontale, l'altro verticale. I due cilindri, di raggio uguale, si intersecano a formare una crociera. Sul punto comune ai due assi si definisce il centro di proiezione. La coordinata X della proiezione sarà ottenuta dal cilindro verticale mentre la coordinata Y si troverà per mezzo del cilindro orizzontale. Si possono individuare almeno quattro metodi per riportare i punti dai cilindri al quadro: ortoproiezione, contro-proiezione stereografica, riporto della lunghezza della corda che unisce il punto con il vertice della crociera (nell'esempio) e il riporto della lunghezza dell'arco di cerchio che unisce il punto stesso sempre con il vertice della crociera. Si noterà che il PP rimane ancora una volta unico (punto di concorso dei segmenti gialli), mentre se si uniscono tra loro gli estremi dei segmenti (linee rosse) si otterrà la caratteristica spina di pesce di cui parla il Panofsky. In altre parole, la "spina di pesce" si ottiene se e solo se si mettono in "prospettiva" esclusivamente i punti estremi dei segmenti che definiscono l'oggetto: se invece i segmenti vengono suddivisi in un gran numero di parti, allora i vari punti si "proietteranno" sul Quadro lungo una linea curva che tenderà ad un unico punto di concorso.

PROSPETTIVA "PANOFSKY" A DOPPIO CILINDRO ELLITTICO. In questo caso, simile al precedente, vengono usati due cilindri a base ellittica anziché circolare. Valgono qui tutte le considerazioni fatte per il caso precedente.

I metodi studiati (anche attraverso altre prove) possiedono tutti la caratteristica comune della concorrenza di linee perpendicolari al quadro ad un unico punto, il PP. Nel caso però della prospettiva proposta da Panofsky, la concorrenza al punto di fuga avviene non per rette (come in tutti gli altri casi) ma mediante archi che appaiono essere funzioni della tangente iperbolica. Avviene quindi una curiosa inversione tra le rette parallele al quadro e quelle perpendicolari ad esso: nel caso di prospettive ottenute per mezzo di un'unica superficie curva (sfera, cilindro, ellissoide od altro) le rette parallele al quadro di norma vengono incurvate nella prospettiva mentre quelle perpendicolari ad esso rimangono rette; il contrario avviene per la prospettiva a "doppio cilindro". 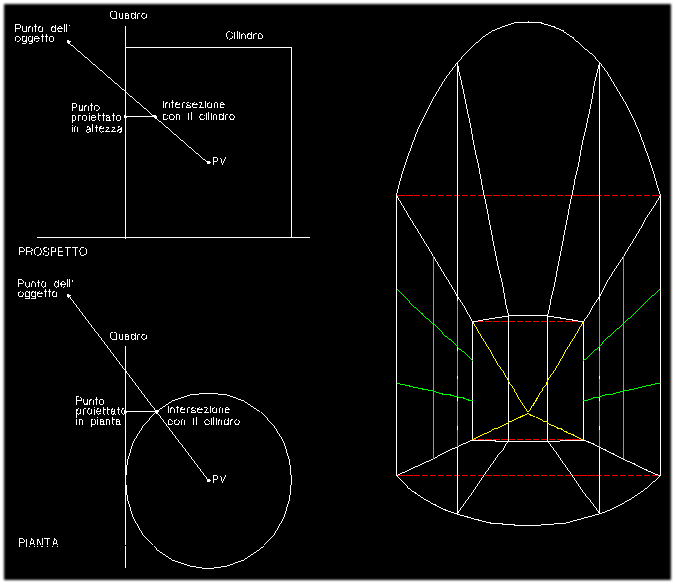In particolare, suddividendo il quadro in settori, come mostrato nella figura (l'immagine a sinistra è ottenuta usando, per i cilindri, un raggio equivalente ad un nono del lato del cubo; nell'immagine al centro un raggio pari ad un terzo del lato e per quella a destra un raggio pari al lato del cubo), e verificando come le rette perpendicolari al quadro verticale concorrono verso il Punto principale, le "curve di fuga" saranno rettilinee nel caso di linee orizzontali o verticali appartenenti ai due piani (orizzontale e verticale) che si intersecano nel PV, o anche nel caso di linee a 45 gradi: questo avviene perché i due cilindri si incontrano nella crociera (e dunque non sussistono due intersezioni tra la retta Occhio-Punto e i due cilindri, ma una soltanto), mentre nei primi due (orizzontale e verticale) le rette giacciono su piani che tagliano perpendicolarmente uno dei due cilindri. Tutte le altre rette ortogonali al quadro vengono incurvate tendendo asintoticamente alle rette che si otterrebbero da una loro prospettiva piana, risultando tanto più incurvate quanto più piccolo è il raggio dei cilindri. Le immagini mostrano l'andamento delle curve di fuga al variare del raggio dei cilindri (ortoproiezione). Gioseffi (cfr. anche la nota 59 del suo Perspectiva artificialis) ritiene poco plausibile tale metodo, oltre che con argomentazioni storico-critiche, anche per la sua scarsa coerenza geometrica: va però rilevato che tale prospettiva non solo, come già visto, mantiene rette le linee parallele al quadro, ma introduce, in generale, deformazioni molto più contenute rispetto agli altri metodi (prospettiva sferica, cilindrica o ellissoidica).

La figura mostra le prospettive, ottenute dal medesimo Punto di Vista, di un cubo inclinato e ruotato rispetto al Quadro verticale in modo da non avere nessuna faccia ad esso parallela. Nelle immagini i segmenti in rosso sono tracciati per rendere conto delle differenze tra i lati deformati (in bianco) e quelli appunto non deformati (in rosso); i segmenti in giallo rappresentano le linee o curve di concorso verso il Punto Principale. L'immagine a sinistra si riferisce al metodo del Panofsky, quella al centro ad una prospettiva sferica stereografica, quella a destra ad una sferica ortografica: è evidente che la prospettiva più "regolare" è proprio quella ottenuta dalla costruzione a "doppio cilindro" proposta dal Panofsky (qui ottenuta con il metodo dell'ortoproiezione).

Le differenze tra i quattro metodi studiati per mettere in prospettiva un oggetto secondo il metodo del Panofsky (ortoproiezione, riporto della corda e suo sviluppo, proiezione stereografica), sono tanto più modeste quanto più grande è il raggio dei cerchi di costruzione: la figura mostra il cubo già considerato (di lato 9 unità) utilizzando cerchi di raggio rispettivamente 1 (colonna sinistra), 3 (centro), 9 unità (destra). La prima riga si riferisce alla proiezione stereografica, la seconda allo sviluppo dell'arco, la terza al riporto della corda e l'ultima alla proiezione ortografica. È interessante notare come la lisca di pesce sia tanto più pronunciata quanto meno profondo è l'oggetto (per profondità infinita esiste, come già fatto rilevare, un unico punto di concorso anche calcolandolo mettendo in prospettiva solo gli estremi dei segmenti, senza suddividerli). Inoltre è evidente come l'utilizzo dei cerchi di proiezione influenzi soprattutto le parti laterali degli oggetti: infatti, per punti che stiano vicini al PP, la curvatura dei cerchi sarà assai poco accentuata. Infine è da notare che, usando cilindri di raggio pari al lato dell'oggetto, anche le linee perpendicolari al quadro risultano quasi rettilinee (colonna a destra).

Ritorno alla pagina principale.

Programma EUCLID per la restituzione prospettica.

	Homepage Camillo Trevisan
	Homepage Istituto Universitario di Architettura di Venezia (IUAV)
	Homepage Dipartimento di Progettazione Architettonica IUAV