Sulla stereotomia, il CAD e le varie trompe d’Anet

Camillo Trevisan
 trevisan@iuav.it

Articolo nel formato PDF (3650 kB)

Saggio pubblicato nel volume
Riccardo Migliari (a cura di), Geometria e Architettura. Strumenti del dottorato di ricerca in Rilievo e Rappresentazione, Gangemi, Roma 2000

Questo breve articolo ha lo scopo di illustrare alcuni aspetti della stereotomia[1], tuttora vivi e degni di attenzione per l’architetto contemporaneo, prendendo come riferimento un manufatto assai notevole – la trompe[2] d’Anet, di Philibert Delorme – e soprattutto le costruzioni geometriche di quella trompe proposte da molti altri trattatisti.[3]
In questa materia, uno dei punti di maggior interesse consiste nell’indagare i sistemi generali ed i procedimenti specifici adottati da ciascun autore per definire, esaminare, verificare, costruire oggetti tridimensionali servendosi di grafici bidimensionali.
In tal senso, si scoprono affinità più penetranti ed estese tra l’attuale modellazione realizzata mediante software CAD e la stereotomia, piuttosto che tra quest’ultima e la stessa geometria descrittiva.
Infatti, lo scopo e l’uso della modellazione solida non è tanto e solo la descrizione dell’oggetto – rappresentandolo in alcune viste congelate, le quali, per identificare univocamente un punto, un segmento, una superficie, richiedono l’una l’esistenza dell’altra – ma piuttosto la determinazione stessa dell’oggetto, costruendone un modello numerico strutturato e topologicamente connesso che potrà essere modificato, esplorato, sezionato, pesato, edificato. Se la geometria descrittiva presuppone l’esistenza di un modello, sia pure mentale, da rappresentare in varie proiezioni, la modellazione solida lo crea.
In altro contesto e per mezzo di tecniche diverse, la stereotomia si assume ed assolve tuttavia lo stesso compito. Un trait géométrique, ancor prima di presentarsi come grafico è un vero e proprio algoritmo, nel quale le variabili di ingresso sono date da una sezione orizzontale ed una verticale del manufatto e l’univoco prodotto è il modello tridimensionale stesso. Un algoritmo nel quale, se i dati di partenza sono corretti e completi, il modello generato non può risultare sconnesso né interpretabile. Un algoritmo, inoltre, dove possono essere ridotti al minimo i parametri iniziali, permettendo all’architetto di concentrarsi sugli aspetti compositivi e morfologici generali, anziché sulle particolarità locali.[4]
La principale differenza tra epure[5] e trait, insomma tra proiezione e nomogramma, risiede soprattutto nel potenziale dinamismo di quest’ultimo, nella sua capacità di modificarsi operativamente, determinando esisti diversi, contenendo sempre in sé, però, tutte le caratteristiche geometriche dell’oggetto.
Sono gli stessi trattatisti, da Delorme[6] a Frézier[7], a suggerire l’uso del trait per la produzione di modelli reali, oltre che come strumento progettuale e costruttivo[8] e base per il taglio dei conci in pietra, i quali, una volta composti assieme, dovranno considerarsi come un tutt’uno.[9]
Ma il dispositivo algoritmico del trait – proprio a causa dell’indissolubile legame istituito tra teoria e prassi, tra progetto e costruzione – pur se univoco, non è tuttavia unico; tanto che molti aspetti in apparenza prettamente geometrici derivano in realtà da necessità costruttive. Una prima lettura trasversale dei grafici qui presentati riguarda infatti la loro costruzione in funzione del sistema di taglio della pietra.Il metodo di taglio par équarrissement (o anche par derobement) è intuitivamente vicino alla generazione di un solido per intersezione di estrusioni, eseguita con programmi CAD. Con altra accezione, può anche essere visto come la riduzione alla fisicità della doppia proiezione ortogonale, poiché ciascun punto è definito dall’intersezione di due o più direttrici, di norma ortogonali tra loro, senza la necessità di conoscere a priori la natura della curva o della superficie alla quale quel punto appartiene. Ed è interessante osservare come lo stesso Frézier descrive il fenomeno: il concio è definito, quasi automaticamente, par une espece de hazard,[10] quasi contrapponendolo al limpido meccanismo del trait.
Di tutt’altra natura il taglio par biveaux.[11] In questo caso ciascuna fase costruisce una faccia del concio (ed è per questo che il metodo è noto anche come directe), poiché, a partire da una prima faccia livellata su di una superficie del blocco e tracciata nel suo contorno sulla scorta del suo panneau,[12] le successive sono legate alle precedenti dalla preventiva conoscenza dell’angolo tra le facce e dei pannelli ad esse riferiti. La generazione del concio in questo caso procede dunque per passi equivalenti, corrispondenti per molti versi alla costruzione di un modello numerico tridimensionale noto come boundary surfaces, nel quale, appunto, ciascuna faccia dell’oggetto individua un’entità grafica, di confine, legata alle altre in una dipendenza ad albero. Infatti, nella costruzione di un tal modello non è indifferente la scelta del percorso generativo, poiché l’uno non è equivalente all’altro ed è sempre necessario conoscere preventivamente l’oggetto in tutte le sue articolazioni, senza lasciare nessuno spazio all’azzardo accennato da Frézier.
Se il primo metodo usa essenzialmente le proiezioni ortogonali, spesso di semplice costruzione, il secondo, richiedendo la conoscenza di angoli generici e dei contorni delle superfici, anche a doppia curvatura, implica dunque ben altri passaggi.Ma è addirittura possibile combinare i due metodi, sfruttandone le singole peculiarità: ad esempio, sbozzando un concio par équarrissement, individuando così alcune facce più semplici, completandolo poi par biveaux, nei recessi meno agevoli.Tale procedimento, noto con il nome di demi-équarrissement, non esaurisce tuttavia tutte le possibilità.
Delorme, infatti, concepisce il trait géométrique forse proprio per superare l’équarrissement, ma spesso riuscendo così ad eludere anche la necessità d’uso di biveaux: nei suoi grafici non esiste nessun riferimento diretto al calcolo preventivo dell’angolo tra due generiche facce contigue di un concio, se non nel caso in cui quest’angolo sia dato per costruzione piana o da un semplice ribaltamento.
In un passaggio di grande interesse egli, infatti, descrive così la fase di taglio di un concio della trompe d’Anet: “Ma voglio ben avvertire il Lettore che i conci di tutti i tipi di trompe sono tra i più difficili da tagliare. Pertanto, dopo aver fatto una faccia al concio per la doile di sotto [l’intradosso della volta della trompe], voi potrete tracciare correttamente il suo cartone; ma per gli altri, per i cartoni de joinct [di giunzione tra i conci], de teste ed anche per i pannelli de doile superiori, guardatevi bene dal tracciarli per tagliare la pietra al primo colpo, perché la rovinereste e non potreste più utilizzarla. È dunque necessario operare un po’ sulla faccia di giunzione, poi un altro po’ sulla parte della testa e similmente sulla parte della doile di sopra e consecutivamente un poco dall’una e un poco dall’altra parte; assolutamente non tutto d’un colpo, ma tagliando così abilmente il tutto, da poter circondare la vostra pietra con i cartoni tutt’intorno fino a farli toccare l’un l’altro alle estremità, sia sui giunti, sia sulle facce e sul davanti, sui pannelli di testa”.[13]
Dunque, per i conci complessi si perviene inizialmente alla costruzione dell’oggetto con metodi semi empirici, nei quali i pannelli svolgono principalmente la funzione di controllo: né è da escludere che i modelli di gesso servissero anche per misurare direttamente gli angoli e per fornire una sagoma reale al tagliatore.
Ma quello non è l’unico passo illuminante. Trattando di una porta sull’angolo (porte & voute sur le coing) egli scrive ancora: “Se volete potete costruire la volta della porta par équarrissement, misurando sulla pianta le lunghezze che dovrete trovare e l’avanzamento di ciascun concio [sull’angolo], senza aiutarvi con i pannelli […] Ma così vi è un gran spreco di materiale e perciò i buoni maestri si servono dei pannelli, mettendoli tutt’attorno alla pietra, per tracciarla in opera, e fanno squadrare la pietra con il biveau, costruito tra il profilo della volta e le linee di giunzione ”.[14]
Ancora, scrivendo sulla vis Saint-Gilles, a proposito degli operai, dice: “Ne ho incontrato qualcuno che la faceva par équarrissement, ma senza alcuna inventiva né industriosità e sprecando molta pietra. Oggidì ne vedo molti che conoscono non solo come costruire la vis Saint Gilles ma molti altri trait.”[15]
Ma immediatamente dopo aggiunge anche: “Se la dovessi costruire io non la farei certo con i pannelli e nemmeno par equarrissement […] È infatti più agevole e facile farla con i biveaux e le sauterelles: poiché avendo le cherches r’alongées [archi di cerchio ‘proiettati’ in forma di archi di ellisse] e gli squadri è facile tracciare [tagliare] tutti i conci”.[16]

Da questi commenti e dai grafici presentati nel trattato di Delorme si deduce pertanto un procedimento di taglio assai flessibile: se i pannelli che circondano il concio sono comunque e sempre descritti e definiti, la fase esecutiva è affidata alle capacità operative dei tagliatori locali. Se questi saranno abili ed ingegnosi, sapranno loro stessi scegliere autonomamente la via più elegante, breve ed economica, nei termini di spreco di materiale.
I trattatisti successivi saranno invece più rigidi, spesso selezionando e descrivendo varie e contrapposte modalità di ‘applicazione del trait sulla pietra’. Ad esempio, la tavola 43 tratta da Frézier (vedi figure 1, 2, 3) illustra limpidamente la complessa sequenza di passaggi necessari per l’identificazione del biveau tra l’intradosso e la superficie di giunzione di un concio di una trompe droite circulaire. Ma anche la figura 4, tratta da de La Hire, e le 5, 6, 7, da Desargues e Bosse, indicano con chiarezza la volontà esplicita di operare soprattutto per mezzo di biveaux.
In tutti i trattati pre ottocenteschi (ad eccezione del Bosse) colpisce, però, la presenza di una moltitudine di casi specifici, selezionati in relazione alla costruzione, al taglio dei conci e ad altre caratteristiche particolari: ad esempio, Derand classifica 27 trompe, 22 descente e quasi un centinaio di altri manufatti, Jousse anch’egli un centinaio, ma lo stesso Frézier, nei suoi tre tomi, ordina la materia anche in funzione dei tipi, così come gli altri trattatisti, i quali presentano i loro lavori quasi in forma di elenco. Tuttavia, nello stesso tempo, la descrizione delle modalità di costruzione del trait passa da semplice ricetta a metodo geometrico codificato e compiuto, anche se sempre meno immediato. Troveranno infatti gli stessi risultati, forse più rapidamente ma anche distaccandosi sempre più dalla realtà e diventando sempre più teorici ed oscuri, oppure generando trait applicabili solo a ristrette categorie di oggetti, sfruttandone le simmetrie e le caratteristiche individuali.
Nei trattati dell’Ottocento, infine, la tassonomia è costruita identificando superfici cilindriche, coniche, sferiche, di rivoluzione e réglé, ottenute per spazzolamento, spesso con ben poche relazioni alle modalità di taglio.
Si assiste dunque ad un lento passaggio da problemi tecnici, legati anche e soprattutto al taglio della pietra, a problemi teorici, geometrici. Le eccezioni, gli anticipati tentativi di ordinamento, sono osteggiati duramente, come accade a Desargues, il quale ha provato a risolvere con gli stessi strumenti i problemi della stereotomia, della gnomonica e della prospettiva.
La celebre disputa sorta tra Curabelle,[17] fiancheggiato dalla comunità del Maestri Massoni di Parigi, e lo stesso Desargues, sostenuto dal suo allievo Bosse, conferma il forte legame allora esistente tra la comunità tecnica e scientifica del tempo e la pratica operativa.Desargues infatti, come nota egli stesso[18] e più tardi anche Frézier,[19] non ha l’ambizione di sovvertire l’art de la coupe des pierres, quanto piuttosto di definire un linguaggio comune e quanto più possibile universale. Le caratteristiche singolari della sua proposta sono, alla fine, alquanto modeste: sistema unico di riferimento, cambiamento dei piani di costruzione, indipendenza della giacitura del concio dalla sua posizione rispetto agli altri conci. Ma usa definizioni tanto innovative (sousessieu, contressieu, traversieu) e, soprattutto, logiche geometriche e proiettive talmente vicine ai teorici - e, perciò, così sospette per i pratici - da essere combattuto per principio.
Gli intenti sono simili, l’interesse e la diversità sono dati principalmente dalla loro ‘applicazione sulla pietra’. È in tal modo probabile che il metodo di Desargues sia stato rigettato anche perché ogni tipo di manufatto ha i suoi specifici problemi tecnici (ad esempio, l’angolo di appoggio dei conci sul trompillon[20], la suddivisione di un arco o di una volta in conci, l’angolo di abbattimento di una pietra); problemi la soluzione dei quali non costituiva certo l’obiettivo primario di Desargues ma che, al contrario, si riverberano ampiamente sul trait costruttivo.
Ricercando, dunque, un percorso di sviluppo dei metodi geometrici adottati nei vari trattati, appare subito chiaro che il procedimento di Delorme è quello più diretto ed aderente alla realtà, come la costruzione legittima del Brunelleschi per la prospettiva. Tutte le sue costruzioni, in apparenza molto varie, sono invece il risultato della combinazione di un piccolo numero di apparati e tracciamenti primari - rotazioni, ribaltamenti, trilaterazioni, definizione di curve per punti – suddividendo un problema complesso in somma di costruzioni più semplici, ad esempio, trovando facilmente la curva di intersezione tra due superfici (vedi figure 8 e 9 e appendice B). Paradossalmente, la prima formulazione del trait géométrique è anche spesso la più chiara e, soprattutto, la più generale, poiché ciascuna curva è descritta per punti ed ogni punto è equivalente agli altri ed è sottoposto alla stessa costruzione, con poche eccezioni.
Ad esempio - prendendo in considerazione le modalità di reperimento delle linee de pente, vale a dire dei pannelli che identificano l’inclinazione e l’estensione dell’intradosso e dell’estradosso della volta -, confrontando le costruzioni di Delorme (figura 8), Bosse (figura 26), De la Rue (figura 14) e Frézier (figura 17) con quelle di Deran (figura 19), Jousse (figura 20), del tardo epigono Boye (figura 21), di De Chales (figura 22) o del Guarini (figura 23, grafico n. 3), si identificano immediatamente due diversi sistemi operativi che pure giungono al medesimo risultato finale. I primi ruotano i cartoni attorno al vertice sino ai bordi della trompe per poi ribaltarli sulla pianta, i secondi li ruotano invece attorno al loro cateto verticale esterno, per ribaltarli sulla pianta attorno al cateto orizzontale. In questo modo, però, i grafici si presentano molto meno chiari e intuitivi: infatti le rette di pendenza dell’intradosso e dell’estradosso dello stesso piano di taglio si incrociano l’una con l’altra, facendo riferimento a due punti distinti tra loro in pianta e avendo pertanto una diversa inclinazione.
Ma se questa differenza può apparire poco importante, in realtà si riferisce ad una precisa volontà di risparmiare spazio su trait, anche a scapito della chiarezza, e soprattutto coinvolge direttamente un altro punto non secondario: i conci termineranno appuntiti oppure manterranno costante il loro spessore? E quale spessore?
L’assonometria della figura 27 illustra questo aspetto, progettuale ma anche costruttivo, dimostrando che esistono varie scelte: usare sempre e solo il punto A, vertice dell’intradosso e dell’estradosso, costruendo così conci acuminati che richiederanno dunque un trompillon, stante l’impossibilità fisica di produrli realmente; adottare ancora il punto A, ma costruire poi cartoni di giunzione con bordi paralleli tra loro (lanciando, dal punto G, la parallela ad AE), non riuscendo però a costruire agevolmente il pannello dell’estradosso; infine, utilizzare vari poli per l’estradosso (ad esempio, il punto B per il pannello illustrato nella figura 27). Ciascuna scelta produce conci con diversa conformazione e altezza, come è mostrato nella figura 28, ed implica procedure geometriche differenziate. Forse non a caso, dunque, molti trattatisti, compreso Delorme, non rappresentano né calcolano i pannelli di sviluppo dell’estradosso.
In tal senso, un interessante confronto sugli obiettivi del trait può essere dato dalla figura 29, tratta da Blanchard, il quale, occupandosi di carpenteria in legno, è più interessato alle sezioni delle travi – alla struttura di sostegno della trompe – che alle linee de pente o ai pannelli di sviluppo.

Da questo pur incompleto e breve esame affiorano tuttavia due questioni che meriterebbero un ben più ampio approfondimento. Due temi per molti versi contrapposti, ma anche complementari, orientati il primo a definire la natura stessa del trait géométrique, il secondo le modalità operative che lo sostengono.
Il trait è uno strumento costruttivo, nello stesso tempo generatore e controllore del modello, un meccanismo unificante che fonde in sé il dualismo progetto/esecuzione. Ma è anche un dispositivo aperto, nel quale possono coesistere metodi disparati, sistemi particolari e intuizioni universali, proprio in virtù della vitalità e nettezza dei suoi obiettivi.
Per questo, ancor più che per le possibili analogie tecniche, sembra avere moltissimi punti in comune con il computer aided design.

 

Appendice A. La trompe di Anet e le sue variazioni ottenute mediante il programma Trompe
Appendice B. Il programma Trompe e il metodo di costruzione del trait proposto da Delorme
Copiare il programma Trompe
 
 

Figure

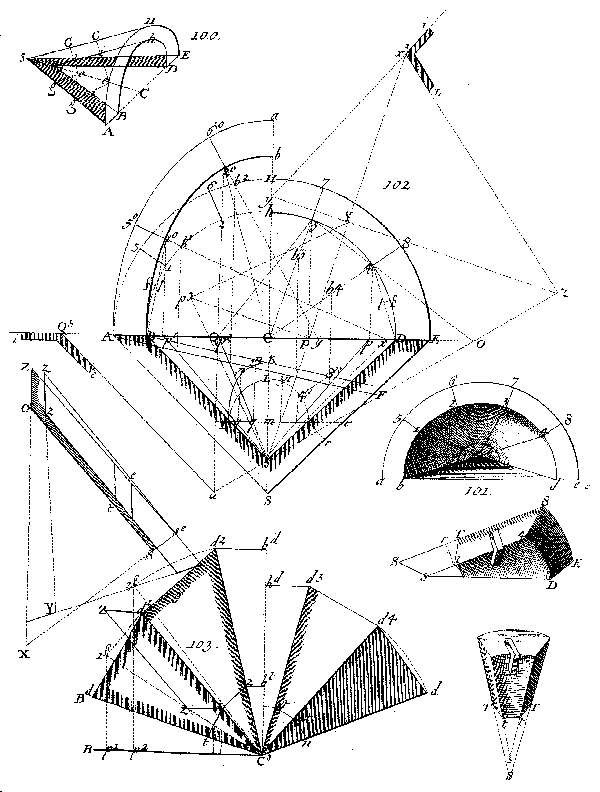Figura 1 
Trompe Droite circulaire. A.-F. Frézier, La théorie…, libro IV, tav. 43, p. 217. Da notare i biveaux posti sui conci e la presenza del trompillon sul vertice della trompe, che influenza la scelta del piano di taglio dei vari conci.
Figura 2
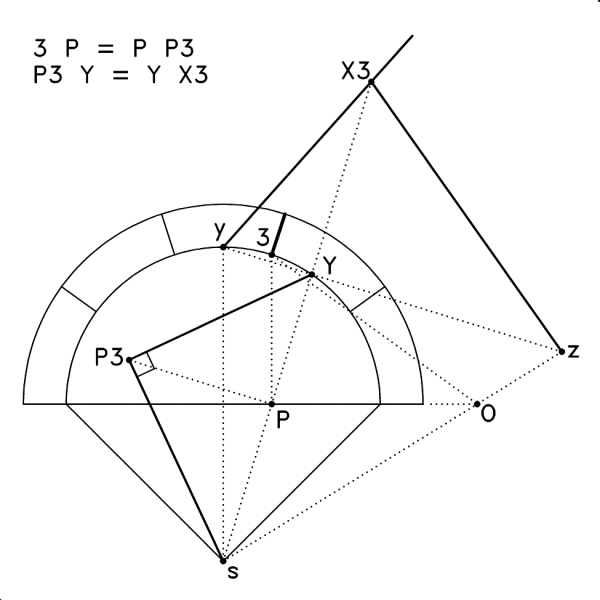
La figura mostra lo schema costruttivo, in pianta, eseguito seguendo le indicazioni del testo e così come è presentato nella figura 1, immagine 102. Da notare la differente posizione dei punti Y e y (sul semicerchio anziché esterni a questo); piccolo errore forse voluto da Frézier per evitare la sovrapposizione di troppe linee sulla semicirconferenza.
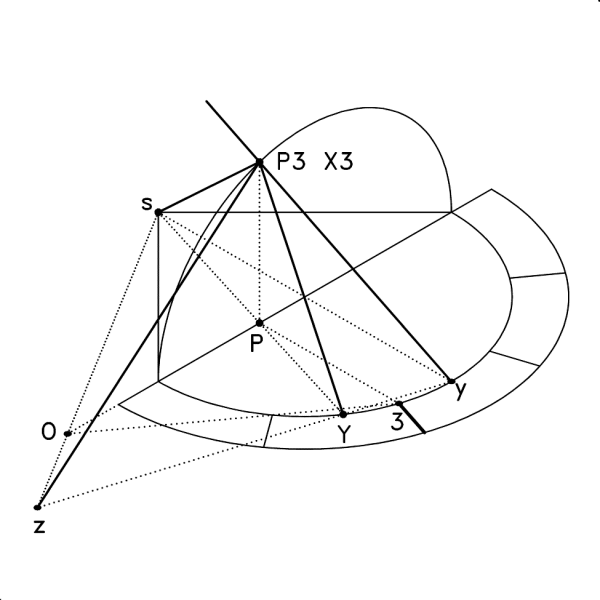
Figura 3
Questa immagine illustra la disposizione tridimensionale dello schema della figura 2: il triangolo s-P3-Y è stato ruotato di 90 gradi sulla retta passante per s e per Y; il triangolo y-X3-z è stato invece ruotato sulla retta passante per y e per z, fino a portare X3 su P3 (sulla verticale per P e sulla superficie dell’intradosso della trompe). Infatti, per costruzione, la distanza tra P e P3 è uguale a quella tra P e 3 e gli angoli s-P3-Y e P3-P-Y sono retti (e dunque P3 ruotato coincide con il punto 3 ruotato di 90 gradi sulla retta per P e per O) e la distanza tra Y e P3 è uguale, sempre per costruzione, alla distanza tra Y e X3. L’angolo trovato (L-x3-i della figura 1, immagine 102) è dunque l’angolo tra il piano di giunzione tra il terzo e quarto concio e la doële plate del quarto concio, misurato sul piano passante per il punto P3 e perpendicolare al piano della stessa doële plate (il piano passante per i punti 3, 4 e s della figura 1, immagine 102).
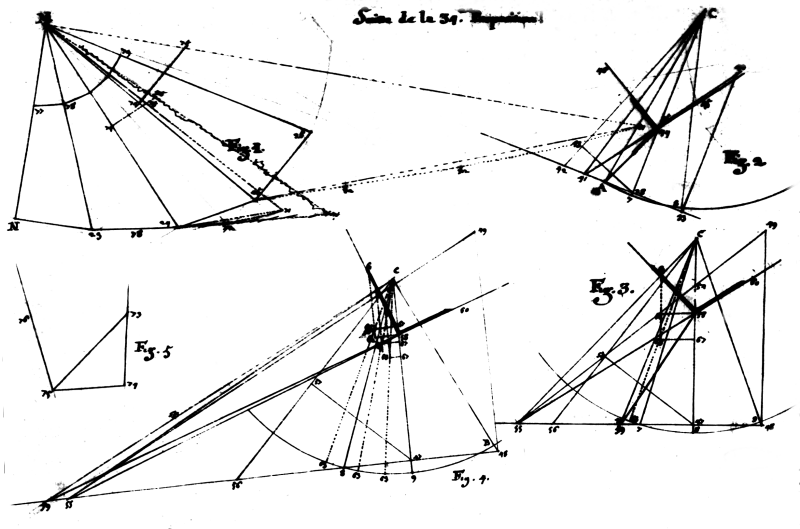
Figura 4
Trouver les panneaux et les Beuveaux des Voussoirs d’une Trompe rampante construite dans un angle rantrant dont les joints de lits sont en ligne droitte, et la teste est courbeé. P. de La Hire, Traité de la coupe des pierres, proposition 34e. Questa figura, tracciata a penna e con alcune correzioni, pur essendo poco chiara dimostra tuttavia la puntuale ricerca degli angoli tra le facce dei conci della trompe.
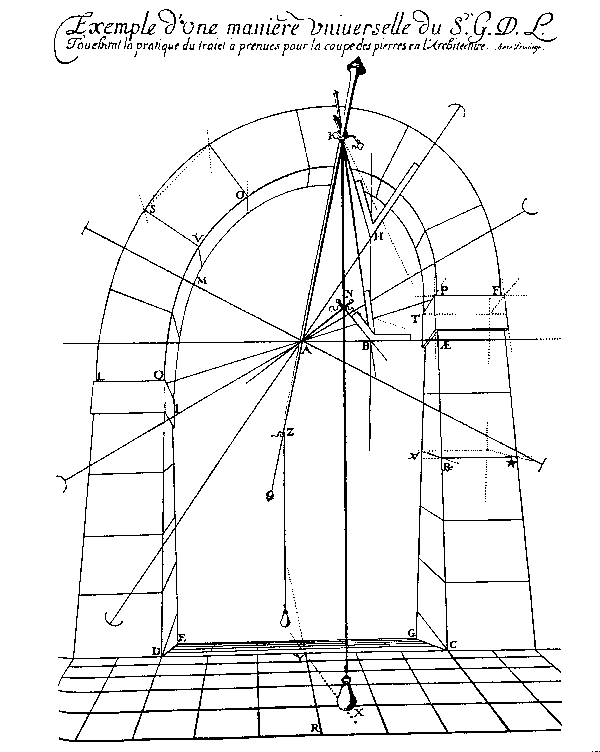
Figura 5
Schema delle rette e degli angoli di una berceau con piano di calpestio e fronte inclinati. G. Desargues, Brouillon project…, tav. 1. La retta KAZ è l’asse (essieu) del berceau; la retta HA è invece il sousessieu, vale a dire l’asse di maggiore inclinazione rispetto al piano di facciata ed una retta, posta anch’essa sul piano della faccia, perpendicolare all’essieu: dunque, la proiezione dell’asse sul piano di facciata. Queste due rette definiscono il piano di facciata: su quel piano, la perpendicolare all’essieu è il contressieu (retta AI), mentre la perpendicolare al sousessieu è il traversieu (retta MA). Da notare anche i fili a piombo KX e in Z, che collegano le rette al sistema di riferimento.
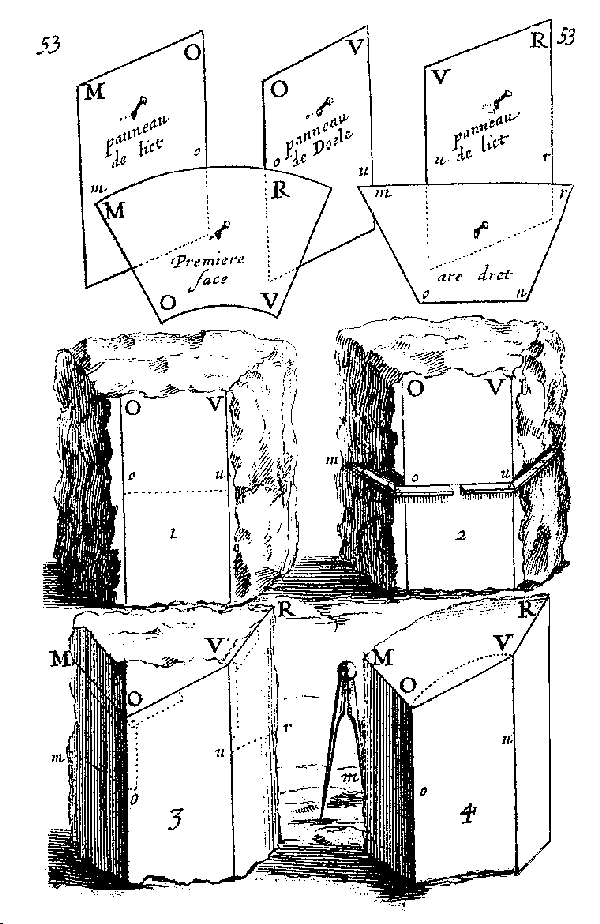
Figura 6 
A. Bosse, La Pratique du Trait, tav. 53. Descrizione dei panneaux e dei biveaux di un concio.
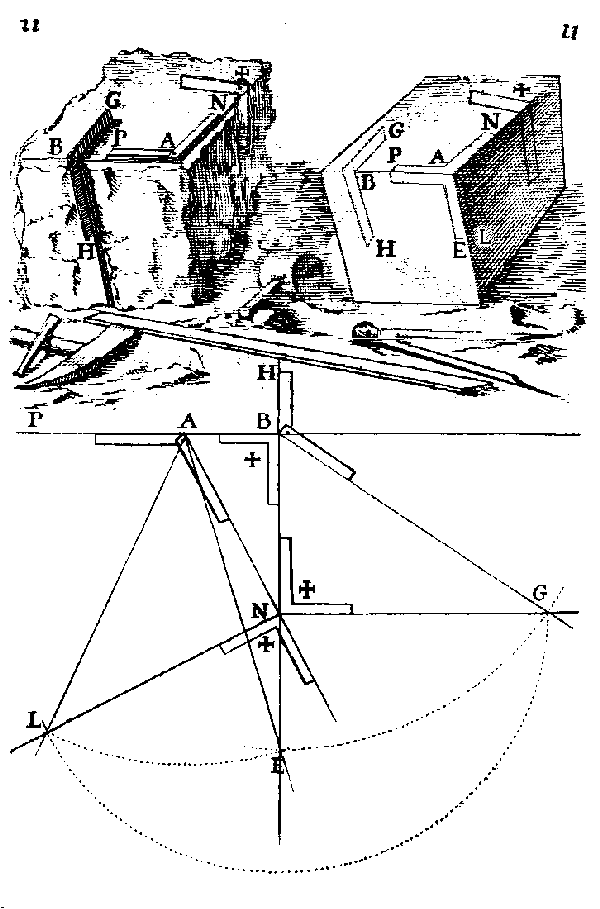
Figura 7 
Prima costruzione per reperire l’angolo des faces nivelée & areste BAE e l’angolo des route nivelée & areste NAL. A. Bosse, La Pratique du Trait, tav. 11.
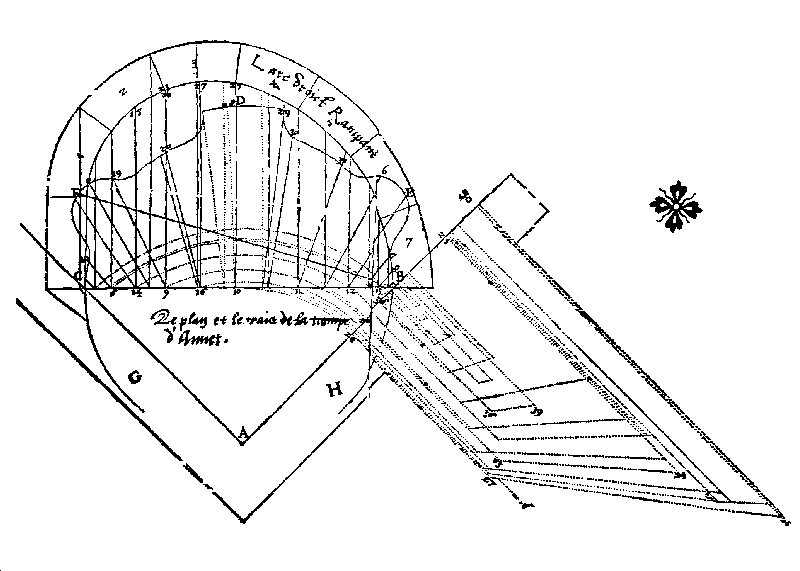
Figura 8
Trait usato per la costruzione dei panneaux della trompe di Anet. P. Delorme, Le premier tome…, ff. 92v.-93r.
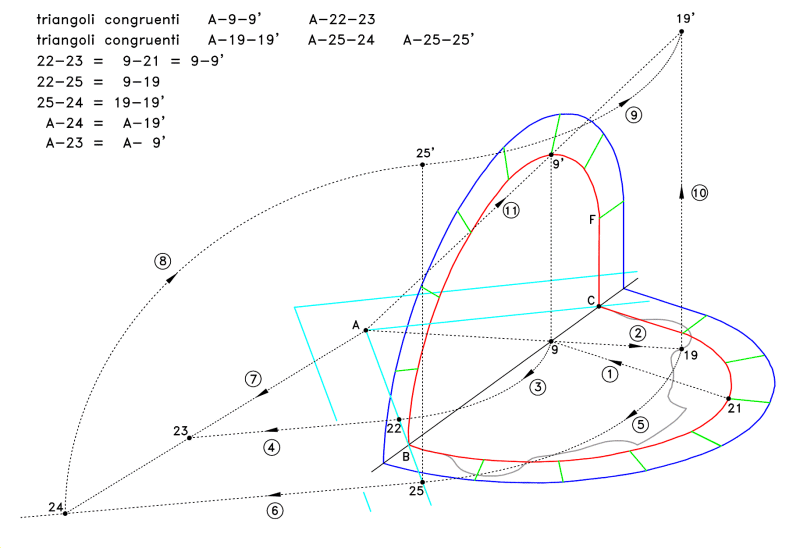Figura 9
Ricostruzione assonometrica del metodo utilizzato da Delorme (vedi figura 8).
Figura 10
Veduta pseudo prospettica della trompe di Anet. P. Delorme, Le premier tome…, f. 89r. Da questa immagine la trompe sembra avere l’intradosso sferico e non conico. Infatti, in quest’ultimo caso la sezione posta sopra la finestra P sarebbe rettilinea e non curva. Tuttavia quella stessa curva potrebbe essere il risultato di una sezione del cono eseguita con un piano, quello del muro laterale, non passante per il vertice. Anche Frézier, che la descrive quando era ancora esistente, la colloca tra le trompe coniche, come del resto si evince dal metodo costruttivo del trait.
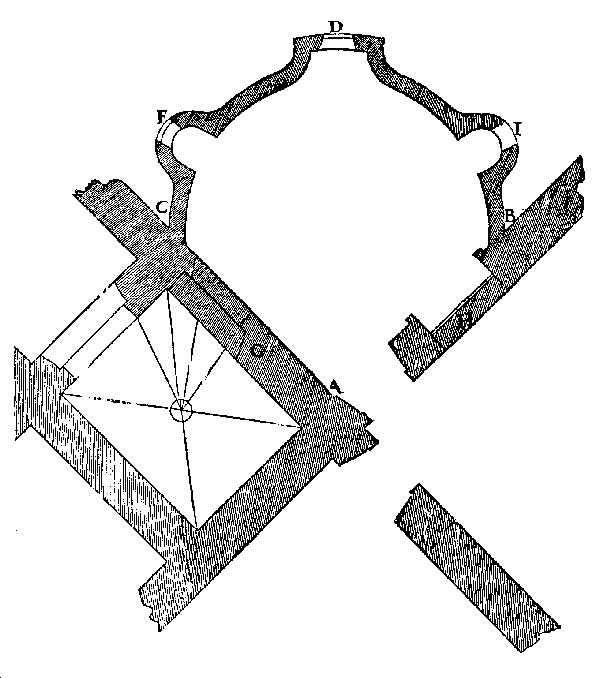Figura 11
Pianta della trompe di Anet. P. Delorme, Le premier tome…, f. 91v.
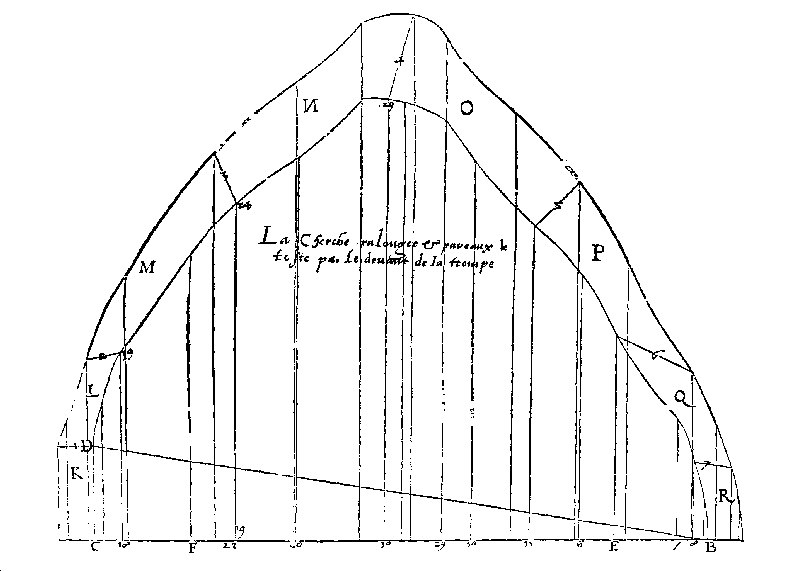Figura 12
Sviluppo frontale della trompe di Anet. P. Delorme, Le premier tome…, f. 94v. Il segmento orizzontale corrisponde, in lunghezza, allo svolgimento del perimetro della pianta della trompe (nel trattato i grafici sono tracciati tutti alla stessa scala rispetto alle probabili dimensioni reali della trompe: 1:18).
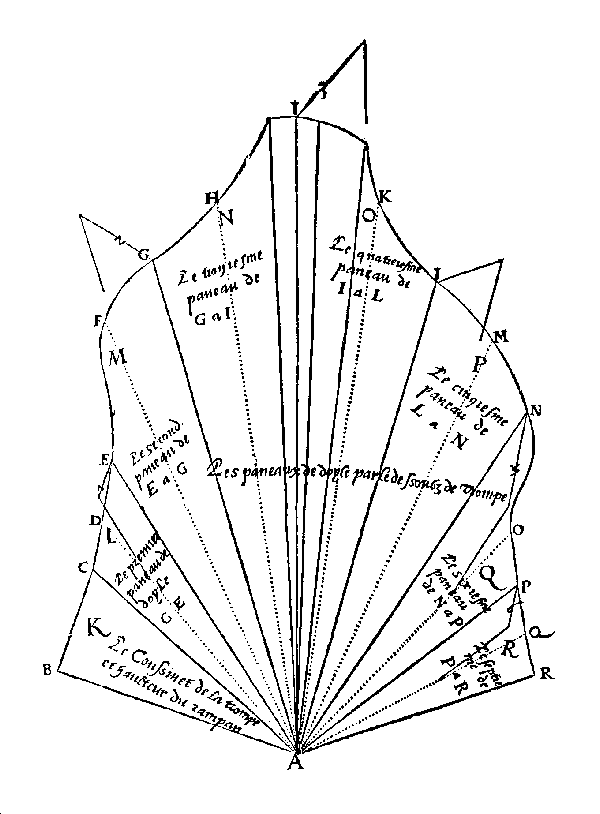Figura 13
Sviluppo della volta inferiore della trompe di Anet. P. Delorme, Le premier tome…, f. 95v. Da notare i pannelli di giunzione ribaltati, definiti con i due bordi paralleli tra loro. La lunghezza della curva è pari alla lunghezza della curva interna del grafico della figura 12, corrispondente al bordo esterno dell’intradosso.
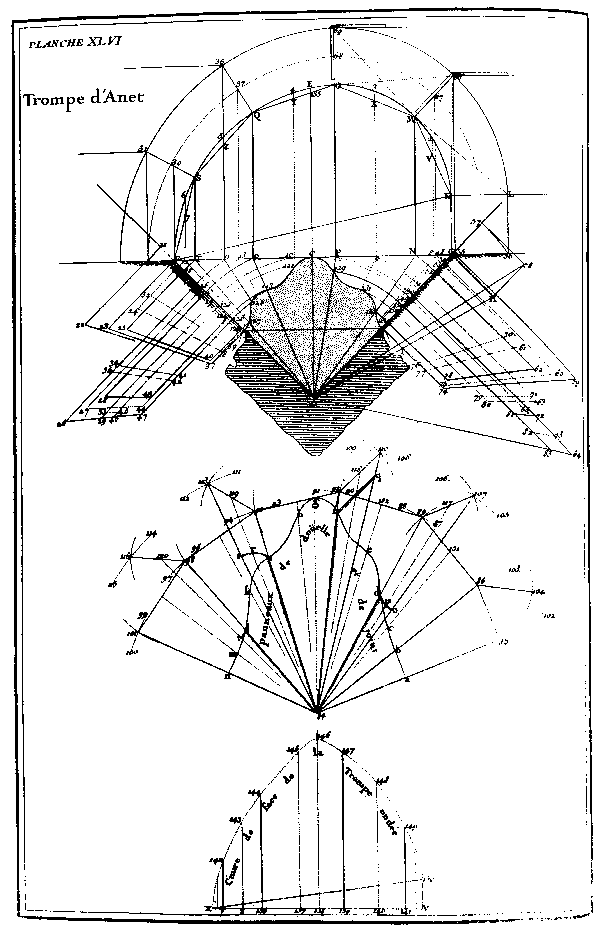Figura 14
La trompe di Anet. J. B. De La Ruë, Traité de la coupe des pierres, tav. XLVI. Da notare i pannelli di giunzione tra i conci triangolari ed il reperimento del vertice superiore per trilaterazione (figura al centro).
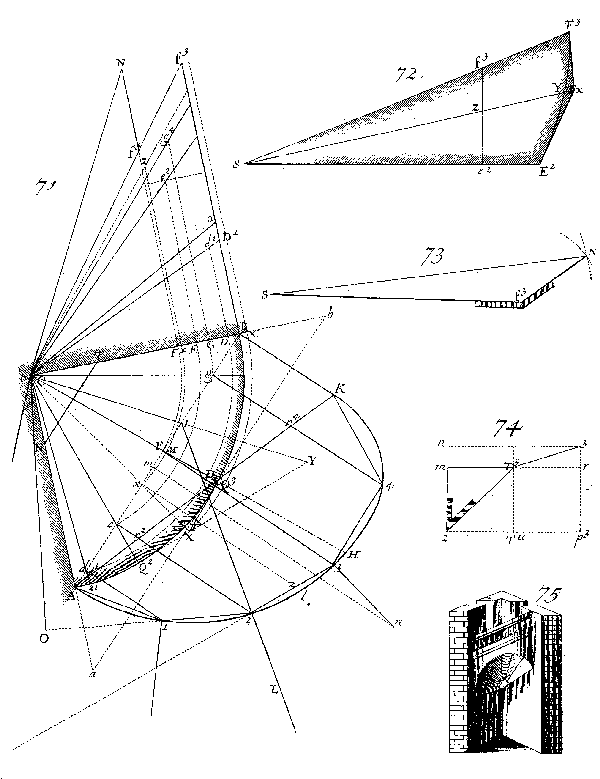Figura 15
Trompe conique rampante en Tour ronde. A.-F. Frézier, La théorie…, libro IV, parte II, tav. 83, p. 113. Anche in questo caso (vedi figura 1) è previsto un trompillon, NT in pianta. Si noti anche il pannello di giunzione triangolare (immagine 73).
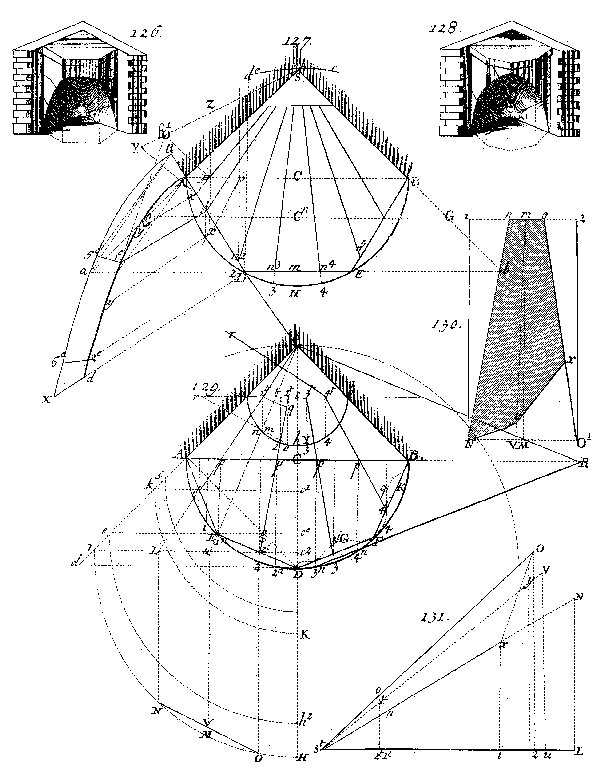Figura 16  
Trompe à Pans e trompe d’Anet non rampante. A.-F. Frézier, La théorie…, libro IV, tav. 48, p. 267. La metà destra del grafico 129 si riferisce ad una trompe d’Anet non rampante, la sinistra ad una trompe à pans: un interessante caso di generalizzazione dei metodi.
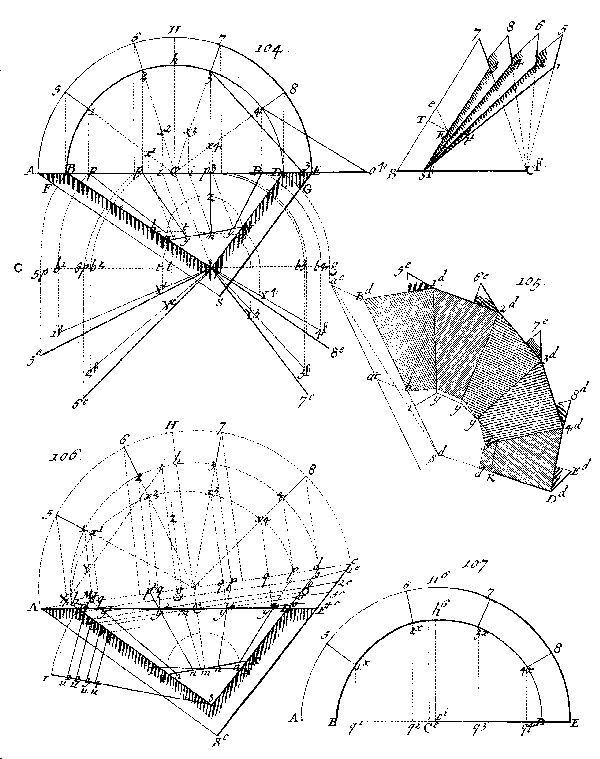Figura 17
Trompe Droite circulaire. A.-F. Frézier, La théorie…, libro IV, tav. 44, p. 229. Si notino i cartoni di giunzione, in alto a destra, con le varie ipotesi di taglio per il trompillon (Ee oppure TE). Da notare anche le rotazioni delle linee de pente.
Figura 18
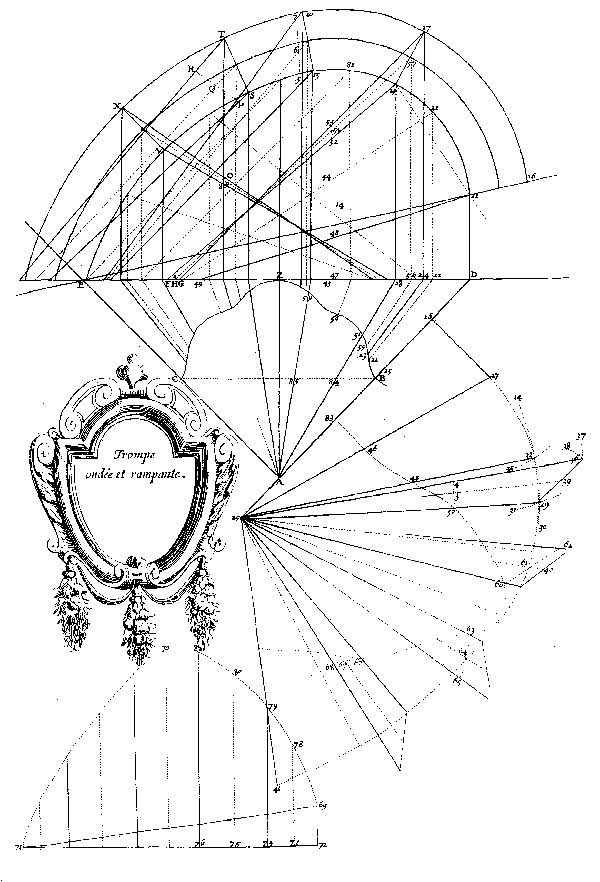
Trompe ondée et rampante. F. Derand, L’Architecture des voutes, cap. XXII, p. 291. Sono qui da notare le rotazioni ed i ribaltamenti delle linee de pente e l’uso di una curva intermedia tra l’intradosso e l’estradosso (oltre ai punti intermedi, posti al centro dei conci), per aumentare la precisione di calcolo (grafico in alto).
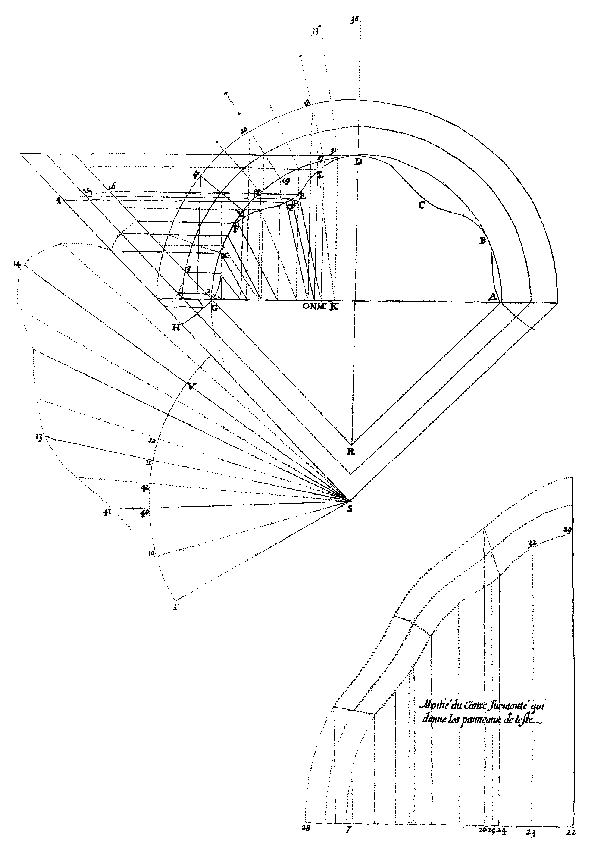
Figura 19
Trompe ondée par devant, ayant son plein cintre. F. Derand, L’Architecture des voutes, cap. XII, p. 259. Da notare, rispetto alla figura precedente, la diversa soluzione adottata per reperire le linee de pente, facendo uso della simmetria e della regolarità della trompe. Viene comunque mantenuta la curva intermedia.
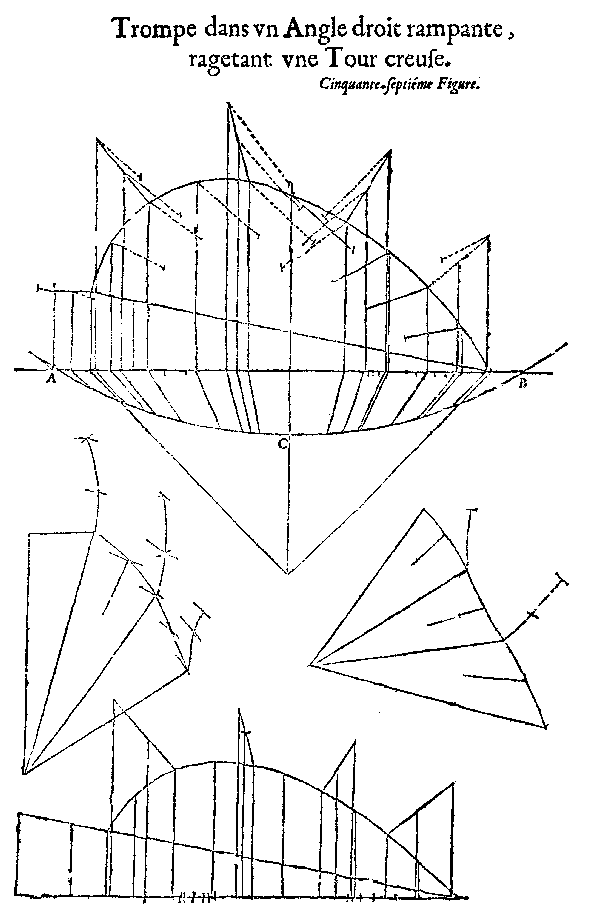Figura 20 
Trompe dans un angle droit rampante ragetant une Tour creuse. M. Jousse, Le Secret d’Architecture, Tav. 57. Anche in questa immagine è interessante notare la modalità di  ribaltamento delle linee de pente e l’uso di una curva intermedia.
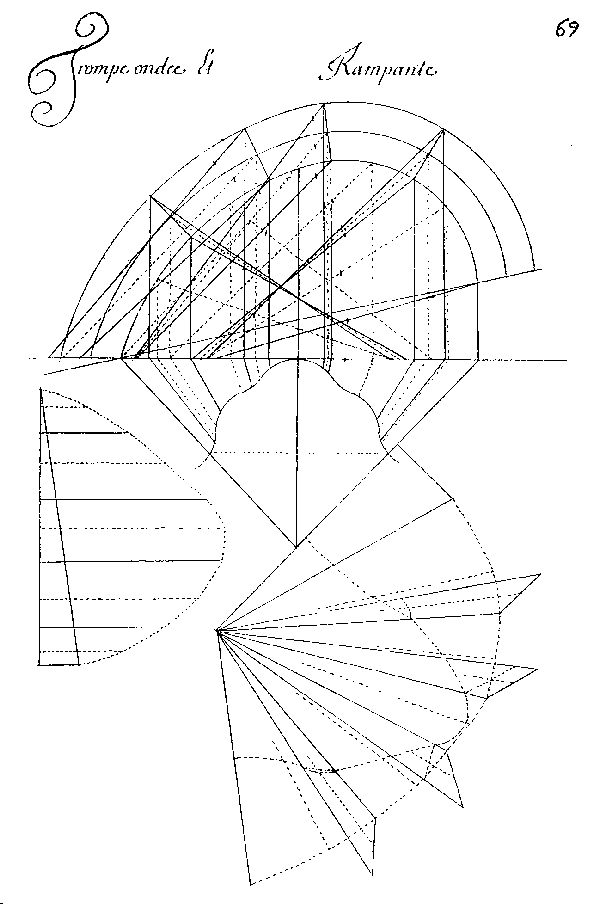
Figura 21
Trompe ondee et Rampante. B. Boye, L’Architecture des voutes, tav. 69. Questa costruzione, tratta da un tardo manoscritto, è del tutto analoga a quella presentata da Derand (vedi figura 18).
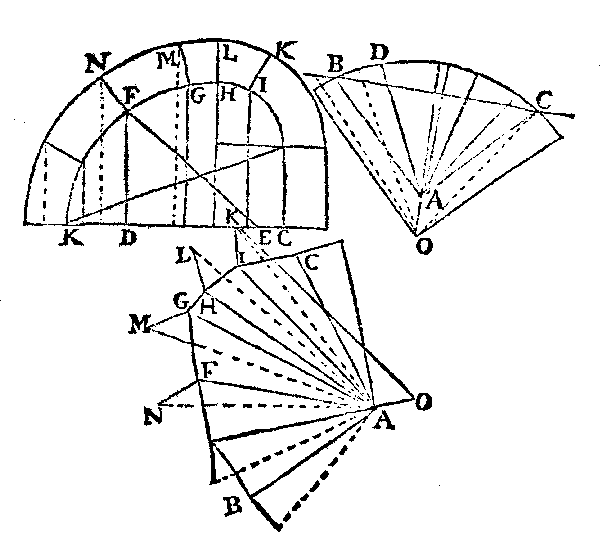Figura 22
Testudo conica pedum inæqualium, cujus ichnographia erit quantum ibet irregularis, & exemplaria frontis æqalia, ovvero della trompe rampante con pianta composta e irregolare oppure regolare. M. de Chales, De lapidum sectione, liber III, propositio VIII. In questa immagine si nota l’uso di un secondo vertice O per l’estradosso (grafico in basso).
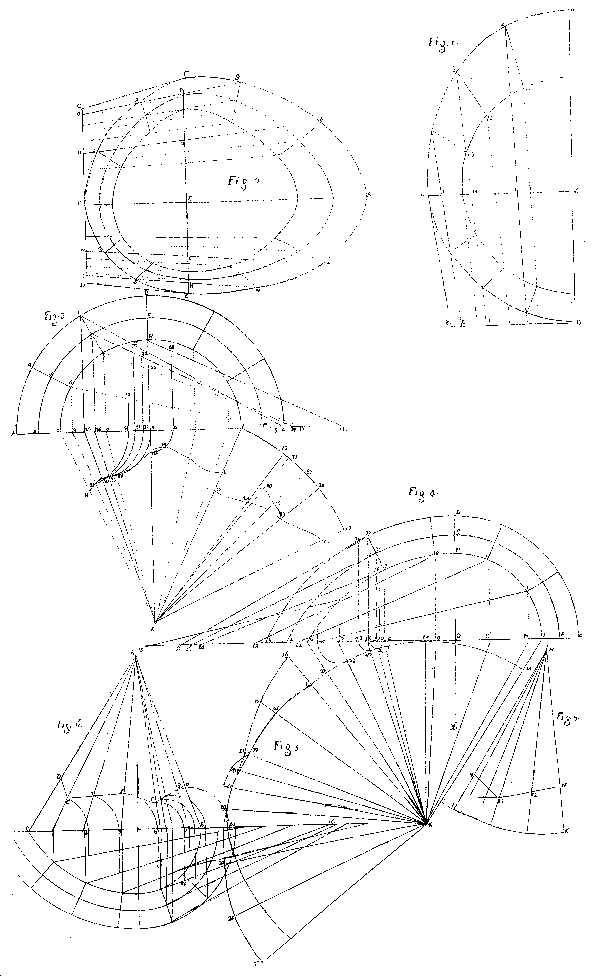Figura 23
La figura 3 si riferisce ad una trompe conica ondée, tagliata da una superficie verticale generica e non piana; Osservazione Nona. Le figure 4 e 5 descrivono un cono a base generica (ellittica, circolare o ‘lenticolare’) segato da una generica superficie verticale; Osservazione Decima. Le figure 1 e 2 si riferiscono rispettivamente ad una trompe conica en talut e ad una trompe biaise. Infine, le figure 6 e 7 si riferiscono ad un cono irregolare, segato da una superficie generica perpendicolare al suo asse; Osservazione Undecima. G. Guarini, Architettura Civile, Tav. XXXIX (corrispondenza edizione originale: Lastra 11, Trattato IV).
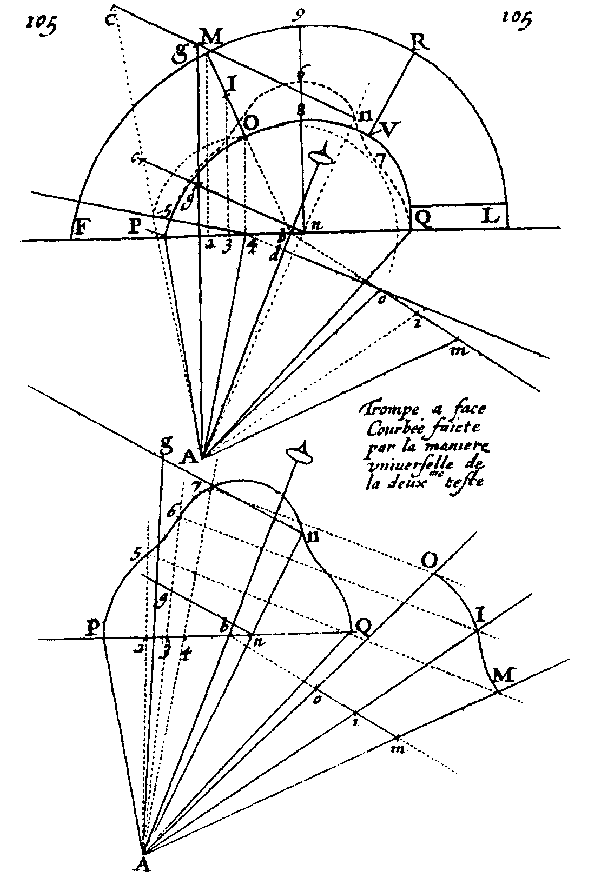Figura 24 
Trompe a face Courbée faicte par la maniere universelle de la deuxme teste. A. Bosse, La Pratique du Trait, tav. 105. Da notare l’uso dell’essieu e delle rette ad esso perpendicolari che identificano il cartone dell’intradosso di un concio.
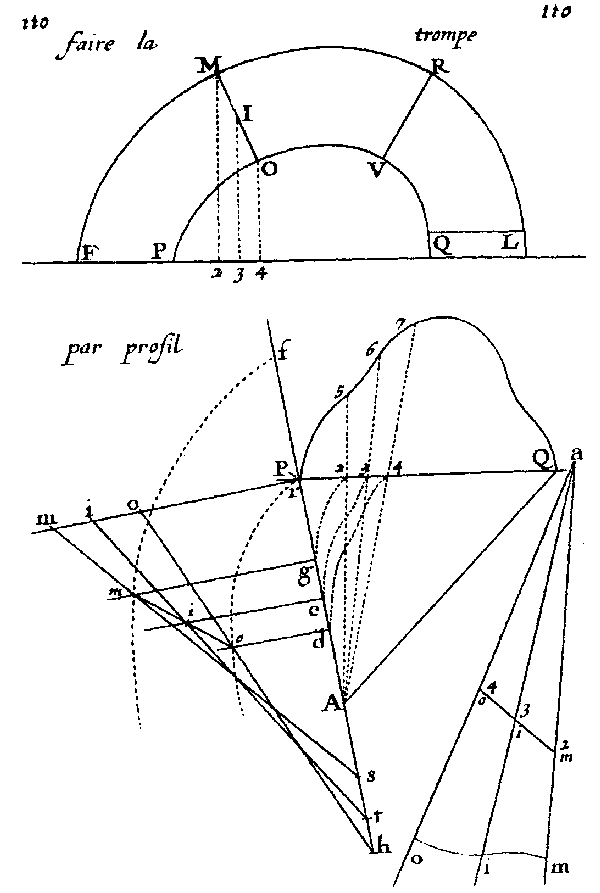Figura 25 
Faire la trompe par profil. A. Bosse, La Pratique du Trait, tav. 110. Da notare la traslazione ed il ribaltamento delle linee de pente del cartone di giunzione MIO (1s corrisponde a 5A, con altezza sul fronte esterno pari a 1M, 1t a 6A, con altezza 1i, ed infine 1h a 7A, con altezza 1o).
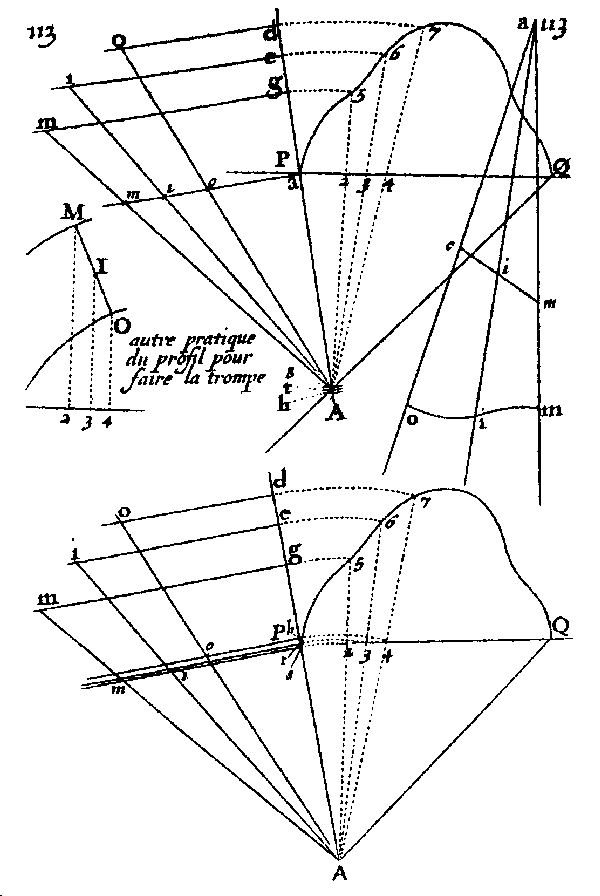
Figura 26 
Autre pratique du profil pur faire la trompe. A. Bosse, La Pratique du Trait, tav. 113. Oltre al ribaltamento delle linee de pente, da notare anche in questo caso (come nella figura precedente) l’uso di una curva intermedia (per il punto I, grafico a sinistra).
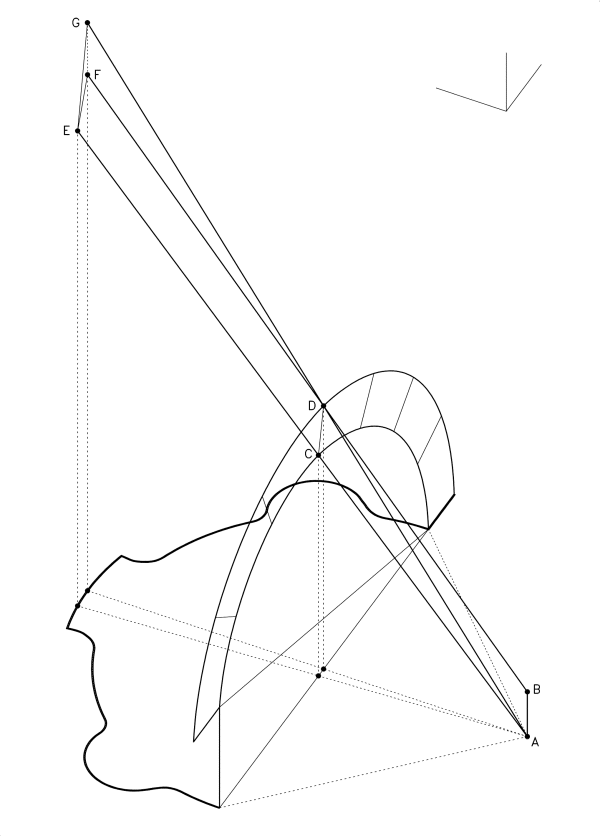
Figura 27
Dimostrazione dei diversi spessori dei conci ottenuti usando due distinti poli di proiezione e sviluppo, A e B. L’immagine illustra le modalità di reperimento delle proiezioni dei punti C e D sul bordo della volta (da notare che le verticali per E, F e G cadono sulla pianta della trompe). Il segmento AE rappresenta il bordo inferiore del cartone (l’intradosso della volta), trovato con il metodo illustrato da Delorme nel suo trattato. Il bordo superiore può essere reperito almeno in due modi. Il primo prevede di usare ancora una volta il polo A: in questo caso il segmento AG rappresenta il bordo superiore del concio; oppure, fissato il punto G, si traccia una parallela ad EA per G, ottenendo così un giunto con bordi paralleli. Il secondo metodo prevede invece di usare un altro polo, ad esempio B, posto a quota superiore rispetto ad A, ottenendo in tal caso il punto F. La retta BF risulta molto meno inclinata di GA rispetto alla retta EA. Da notare però che, se B è posto sulla verticale di A, il giunto non sarà piano: perché questo avvenga è dunque necessario che il punto B si trovi sul piano per i punti A, C e D.
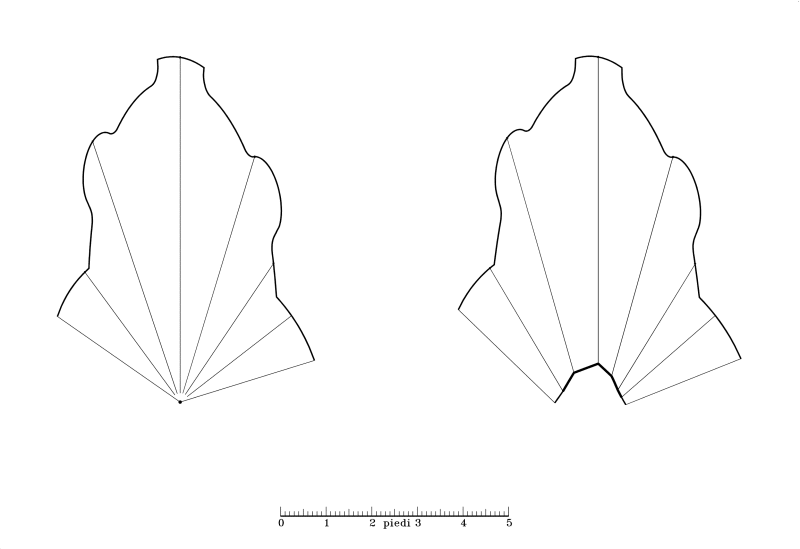
Figura 28
Confronto tra i pannelli di sviluppo dell’estradosso, ottenuti entrambi per mezzo del programma Trompe (vedi appendice B). Il pannello di sinistra è ottenuto usando il punto A come polo di sviluppo anche per il cartone dell’estradosso. Quello di destra è invece ottenuto con l’uso di poli superiori coordinati per lo sviluppo dell’estradosso e prevede che gli spessori dei conci siano costanti (anche se non necessariamente uguali tra loro).
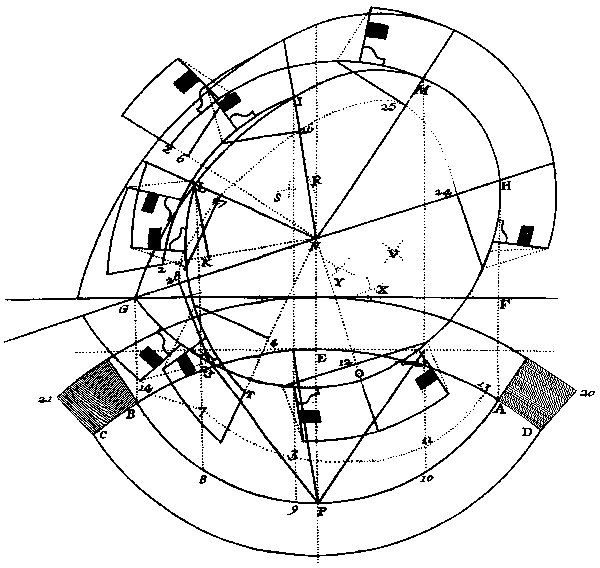Figura 29
Des Trompes rampantes & enniches, E. Blanchard, Traité de la Coupe des Bois..., tav. 26, pp. 63-4. Il grafico posto in alto rappresenta la sezione verticale per AB, traslata e ribaltata in pianta. La curva punteggiata, passante per i punti 24..28, definisce la proiezione sul fronte dei conci in legno che generano la curva rampante e permette di identificare le misure lorde dei blocchi di legno di partenza.

Note

Ringrazio moltissimo il prof. Riccardo Migliari per questo invito.
Le considerazioni che seguono sono frutto di uno studio su alcuni trattati che, tra la seconda metà del Cinquecento e la prima metà del Settecento, hanno posto le basi e definito la stereotomia. I risultati complessivi, di prossima pubblicazione con il titolo Per la storia della stereotomia. Geometrie, metodi e costruzioni, sono disponibili anche in Internet, limitatamente all’apparato critico, alla pagina: http://www.iuav.it/dpa/ricerche/trevisan/stereo/stereo.htm

[1] Per un’analisi più estesa e approfondita della stereotomia si veda: Jean-Marie Pérouse de Montclos, L’architecture à la française, XVIe, XVIIe, XVIIIe siècles, Picard, Paris 1982; Joel Sakarovitch, Théorisation d’une pratique, pratique d’une théorie. Des traitées de coupe des pierres à la géométrie descriptive, tesi di dottorato, École d’Architecture de Paris La Villette, 1989; Philippe Poitié, Philibert Delorme: figures de la pensée constructive, Parenthèses, Paris 1996; Yves Deforge, Le graphisme technique, son histoire et son enseignement, Editions du Champ Vallon 1981, pp. 48-55; Robin Evans, The Projective Cast, MIT Press, Cambridge Mass. 1995, pp. 179-239; Werner Mueller, Guarini e la stereotomia, in ‘Guarino Guarini e l’internazionalità del barocco’, Torino 1970, vol.1, pp. 531-56.
[2] La trompe è una piccola volta che sopporta una copertura o un muro a strapiombo. Spesso le imposte di una trompe sono costituite da due muri posti ad angolo retto (trompe dans l’angle), ma non sono rari i casi di angoli acuti, ottusi o di imposta unica con andamento curvo o rettilineo (trompe sur le pan). Per definire la collocazione tassonomica di una trompe è opportuno considerare, in prima istanza, tre elementi variabili: le sezioni orizzontali inferiore e superiore e la sezione verticale trasversale, vale a dire la pianta dei muri d’imposta, quella della costruzione sostenuta dalla trompe e la sezione dell’intradosso della volta. Questi grafici costituiscono anche la base del trait, il tracciato costruttivo della trompe stessa. Per la classificazione di una trompe si ricorre dunque alla specificazione del tipo di muratura sottostante la trompe ed a quella della costruzione soprastante, spesso con l’aggiunta del tipo di intradosso. Quest’ultimo potrà essere piatto (plate, in realtà leggermente curvo e dunque plate cylindrique o plate sphéroïdale), conico (conique, en canoniere), sferico (sphérique, en cul-de-four), cilindrico (cylindrique, en berceau o en demi-berceau), rampante, misto o di altro tipo ancora. Ad esempio, una trompe dans l’angle e sous le coin indica una costruzione posta tra due muri ad angolo, che sostiene un cabinet quadrangolare, il quale forma un angolo sporgente (coin). Una trompe sur le pan e sous le coin è invece posta su un muro che costituisce l’ipotenusa di un triangolo che ha per cateti i due muri ad angolo, sporgenti, sostenuti dalla trompe (tipicamente questa trompe ha l’intradosso cilindrico). Una trompe plate cylindrique sur le pan et en tour-ronde si appoggia su un muro diritto (sur le pan), ha l’intradosso cilindrico e sostiene una costruzione con sezione orizzontale semicircolare o semiellittica (en tour-ronde). Se il suo fronte è concavo (verso l’interno) la trompe è invece en tour creuse. Una trompe sphérique dans l’angle et sous le coin, è caratterizzata da un intradosso sferico, posto su due muri ad angolo, che sostiene un cabinet quadrangolare. La trompe di Montpellier, dalla forma più semplice tra tutte, è caratterizzata invece da una sezione orizzontale ed una verticale trasversale entrambe a semicerchio e insiste su due appoggi posti ad angolo retto: è dunque una trompe conique dans l’angle et en tour-ronde. Deran, infine, chiama trompe fondamentale la trompe conica retta (conique droite, dans l’angle), vale a dire una trompe nella quale il fronte è piano e verticale (generalmente posto a 45 gradi rispetto alle imposte), mentre l’intradosso e conico: caratterizzata da un trait di semplice definizione, verrà spesso utilizzata come contenitore di trompe più complesse, come quella rampante et ondée di Anet.
[3] Le immagini e i metodi qui illustrati si riferiscono ai trattati di Edme Blanchard, Traité de la Coupe des Bois pour le revêtement des Voutes, Arrières-Voussures, Trompes..., Josse et Jombert, Paris 1729; Blaise Boye, L’Architecture des voutes, Biblioteca Municipale di Bordeaux, inv. Ms. 619, 1741; Abraham Bosse, La Pratique du Trait a preuves de Mr. Desargues pour la Coupe des pierres en L’architecture, Paris 1643; Claude François Milliet de Chales, De Lapidum Sectione in Cursus seu mundus mathematicus, Lyon, 1674; Philibert Delorme, Le premier tome de l’architecture, Paris 1567 (succ. 1568, 1576, Rouen 1648, 1894, Bruxelles 1981); François Derand, L’Architecture des voûtes, Paris 1643 (succ. 1743, 1755); Girard Desargues, Brouillon project d’exemples d’une manière universelle du sieur G.D.L., touchant la pratique du trait à preuve pour la coupe des pierres en architecture..., Paris 1640; Amédée-François Frézier, La théorie et la pratique de la coupe des pierres et des bois..., 3 vol., Strasbourg-Paris 1737-39 (succ. 1754, 1769, 1980); Guarino Guarini, Architettura civile, postuma, 2 vol., Torino 1737 (succ. London 1964, Milano 1968); Mathurin Jousse, Le Secret d’Architecture, decouvrant fidelement les traits Géométriques, Couppes, & Dérobemens necessaires dans les Bastiments, La Flèche 1642 (privilège del 1635); Philippe de La Hire, Traité de la coupe des pierres, ms n. 1596 Bibliothèque de l’Institut de France, Paris; Jean Baptiste De La Ruë, Traité de la coupe des pierres, Imprimerie Royale, Paris 1728 (succ. 1764, 1858).
[4] Si veda: C. Trevisan, Le proporzioni nascoste nel trait della trompe di Anet, in ‘Disegnare idee immagini’, n. 16 (1998), pp. 59-66.
[5] L’épure è un grafico in scala naturale, eseguito di norma su di una superficie orizzontale o verticale, con funzione di riferimento per il taglio e la dislocazione dei conci di pietra di un arco, una volta, una finestra o una colonna.
[6] “Il suffit donc à l’Architecte de savoir bien faire ses lignes pour dresser proprement un plan, & une montée faicte nettement avec toutes ses proportions & mesures, afin que le Seigneur l’intende. Puis dresser ses modelles qui seront de bois ou papier, ou de charte, ou d’autre maniere, ainsi qu’elle luy viendra à propos”. P. Delorme, Le premier tome…, f. 22v.
[7] “On dit couper du trait pour exprimer l’étude que l’on fait avec de la craye, du platre au autre matiere facile à couper, qu’on taille en petits voussoirs de la même maniere que si on exécutoit une voûte en grand, pour apprendre à joindre la theorie à la pratique, & concevoir plus facilment l’effet des Traits dont on s’est servi, soit aussi pour sentir le plus ou le moins de commodité des differentes manieres qu’on a inventé en se servant des panneaux ou en taillant par équarrisement”. A.-F. Frézier, La théorie…, libro I, pp. 408-9, voce Trait.
[8] “Quand il y a quelque difformité, communement les Maçons, pour n’entendre l’artifice des dicts traicts, ils font les voûtes de brique ou de moilon, & de pierres menues, plustost que de pierre de taille, pour n’avoir point l’industrie de les y accommoder, & sans y espargner le plus souvent de grandes barres de fer, pour soustenir leurs Maçonneries, de peur quelles ne tombent; qui est une tres-mauvaise coustume & façon, pour les raisons que nous avons dictes ailleurs”. P. Delorme, Le premier tome…, f. 68r.
[9] P. de La Hire, Traité…, f. 1.
 [10] A.-F. Frézier, La théorie…, tomo II, libro IV, p. 13.
 [11] Il biveau è la sagoma dell’apertura di un angolo qualunque - rettilineo, curvilineo o, più sovente, misto - per indicare l’angolo tra due superfici che si incontrano. Se queste sono piane, ci si serve, per il biveau, di una sauterelle o di una fausse équerre a stecche mobili; se invece una delle due superfici è curva o lo sono entrambe, il biveau è uno strumento di legno, fisso, fatto appositamente per quell’angolo. Definizione tratta da A.-F. Frézier, La théorie…, libro I, pp. 392, voce Biveau.
 [12] Il panneau è la sagoma di una delle superfici di un concio, tagliata in legno, cartone o altro materiale sottile, per essere applicata sulla pietra e per tracciare i contorni di un Lit, di una Doele o di una Tête, da cui i nomi di pannelli de lit, ecc. (definizione tratta da A.-F. Frézier, La théorie…, libro I, pp. 403, voce Panneau). Il pannello potrà riferirsi ad una superficie piana oppure curva e sviluppata sul piano.
 [13] “Mais ie veux bien advertir le Lecteur que les pierres de toutes fortes de trompes, sont plus difficiles a tailler que de beaucoup d’autres fortes de traicts, pour autant qu’apres avoir fait un parement à la pierre pour la doile de dessus, vous pouvez bien trasser son paneau justement; mais pour les autres, comme pour le paneaux de joincts, paneaux de teste, & aussi paneaux de doile par le dessus, gardez-vous bien de le trasser pour coupper la pierre du premier coup, car vous la gasteriez, & ne pourroit plus servir. Il faut doncques oster un peu d’un des joincts, & puis un peu du costé de la teste, semblablement du costé de la doile de dessus, & ainsi consequemment un petit de l’un & petit de l’autre, & non point tout à un coup, mais couppant si dextrement le tout, que vous puissiez armer votre pierre de paneaux tout autour qui se rapportent justement, & se touchent l’un l’autre par toutes leurs extrémitez, tant par les joincts que par les doiles & par le devant, où est le paneau de teste; car si vous n’y preniez garde, votre pierre seroit incontinent gastée, & ne pourroit servir”. P. Delorme, Le premier tome…, f. 99r.
 [14] “Si vous voulez vous pouvez faire telles voûtes de porte par équarissement, en observant les longueurs que vous devez trouver sur le plan et prenant les avancements d’une chacune pièce, sans vous y aider des paneaux [...] Mais en cela il y a grande perte de pierres qui fait que les bons maistres se servent du paneau, lequel ils mettent tout autour des pierres pour les trasser quand ils veulent bien faire selon le traict & oeuvre qu’ils ont à suivre: & font équarrir leurs pierres avecques le buveau qui est faict après la voute & les lignes qui monstrent les comissures”. P. Delorme, Le premier tome…, f. 73v. In questo caso l’accenno al biveau si riferisce ad un angolo ricavabile direttamente da un ribaltamento sulla pianta.
 [15] ”On en rencontroit quelques uns qui la faisoient par équarrissement, mais en cela n’y a gueres d’esprit ni d’industrie, et y faut prendre beaucoup de pierre. Auiourd huy i’en voy plusieurs qui entendent non seulement la façon de ladicte, mais aussi plusieurs autres bons traicts”. P. Delorme, Le premier tome…, f. 123v.
 [16] “Si ie l’avois à conduire ie ne me soucierois gueres de la faire par paneaux, ny moins par equarrissement, vous advisant qu’il n’y a point tant de peine, ny tant de difficulté que les ouvriers le pensoient  pour lors, et que plusieurs encores le pensent, pur ne le sçavoir. Il est aussi fort aisé et facile de la faire avec des buveaux et sauterelles: car en ayant les cherches r’alongées qu’il y faut, et leurs equierres, il est facile d’en trasser iustement toutes les pierres”.  P. Delorme, Le premier tome…, f. 124r.
 [17] Jacques Curabelle, che Frézier giudica un critico ignorante, nel suo Examen des oeuvres du Sieur Désargues del 1644, lanciò un violento attacco al lavoro di Desargues, sia sui temi di stereotomia, sia sulla prospettiva e la gnomonica. Desargues allora scrisse il pamphlet: Récit au vray de ce qui a esté la cause de faire cet escrit, Paris 1644. In esso inserì inutilmente molti nuovi dettagli inediti sul suo lavoro e sulle sue teorie. Tra l’altro, riferendosi a Curabelle, Desargues scrive: “Moi, je ne suis artisan de la main d’aucune sorte d’Art; je n’ai que la simple connaissance de la raison de l’effet des règles du peu de traits dont je propose la pratique; et je n’ai point une cabale d’ouvriers comme il a ses compagnons [...]; par le nombre et par la crierie desquels il voudrait m’opprimer; et comme il sait que je ne travaille point de la main, il me voudrait engager à quelque travail effectif de maçonnerie ou bien à dépendre de la discrétion des ouvriers, ses compagnons de coterie; ce qui ne serait ni juste ni rasonable”. Desargues citò anche Curabelle in giudizio, ma senza successo.
 [18] Lo stesso Desargues, nella prima pagina del suo Brouillon project, scrive infatti: “on trouvera [...] que dans celui de la perspective, il n’y a rien qui tende à se faire passer pour une perspective nouvelle ou autre que celle qui est partout imprimée, non plus que celui-ci du trait ne tend pas à passer pour une nouvelle coupe des pierres, et que tous deux ne tendent à passer que pour exemple d’une manière de pratiquer chacun de ces Arts, nouvelle au moins en quelque circonstance, et surtout aisée et en main au commun des ouvriers, auxquels ce n’est pas le meilleur de proposer une tant sublime Géometrie”.
 [19] A.-F. Frézier, La théorie…, tomo II, libro IV, capitolo V, pp. 191-206.
 [20] Il trompillon è il piccolo concio, posto sul vertice della trompe, che raccoglie le teste interne di tutti i conci che in esso convergono. In tal modo, i conci radiali, anziché terminare appuntiti e pertanto fragili, possono appoggiarsi al trompillon con una testa piatta.

 

Homepage Camillo Trevisan

Homepage Istituto Universitario di Architettura di Venezia

Homepage Dipartimento di Progettazione Architettonica

Visitatori dal 15 Luglio 2000          Ultimo aggiornamento: 15 Luglio 2000